Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(l\) là chiều dài lò xo lúc ko biến dạng \(\Rightarrow\left\{{}\begin{matrix}l_{max}=l+A=30\\l_{min}=l-A=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}l=25cm\\A=5cm\end{matrix}\right.\)
Khi lò xo dài 30cm, tức là vật đang ở biên dương, độ lớn của gia tốc là 8m/s^2\(\Rightarrow\left|a\right|=\omega^2A=800\left(cm/s^2\right)\Leftrightarrow\omega=\sqrt{\dfrac{800}{A}}=\sqrt{\dfrac{800}{5}}=4\pi\left(rad/s\right)\)
Gốc thời gian là lúc vật qua O theo chiều âm, tức là pha ban đầu bằng pi/2
\(\Rightarrow x=5\cos\left(4\pi t+\dfrac{\pi}{2}\right)\left(cm\right)\)
b/ \(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
Nghĩa là khi vật qua vị trí có li độ là \(\left[{}\begin{matrix}x=-2,5cm\\x=2,5cm\end{matrix}\right.\)
c/ Góc vật quay được trong thời gian delta t là: \(\varphi=\omega.\Delta t=4\pi.\Delta t\left(rad\right)\)
Quãng đường lớn nhất đi được khi vật chuyển động xung quanh vtcb
\(S_{max}=2A.\sin\left(2\pi.\Delta t\right)\)
Quãng đường nhỏ nhất đi được khi vật chuyển động xung quang biên
\(S_{min}=2A-2.A\cos\left(2\pi.\Delta t\right)\)
\(\Rightarrow S_{max}-S_{min}=2A\left(\sin\left(2\pi.\Delta t\right)-1+\cos\left(2\pi.\Delta t\right)\right)\)
Xét \(M=\sin\left(2\pi.\Delta t\right)+\cos\left(2\pi.\Delta t\right)=\cos\left(2\pi\Delta t-\dfrac{\pi}{2}\right)+\cos\left(2\pi\Delta t\right)=2\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}+2\pi\Delta t}{2}\right)\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}-2\pi\Delta t}{2}\right)\)
\(M=2\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)\cos\left(\dfrac{\pi}{4}\right)\)
Để \(\left(S_{max}-S_{min}\right)_{max}\Leftrightarrow M_{max}\Leftrightarrow\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow2\pi\Delta t-\dfrac{\pi}{4}=0\Leftrightarrow\Delta t=\dfrac{\pi}{4.2\pi}=\dfrac{1}{8}\left(s\right)\)
d/ Ta thấy vật N luôn dao động vuông pha với vật M
\(\Rightarrow\left(\dfrac{x_M}{A_M}\right)^2+\left(\dfrac{x_N}{A_N}\right)^2=1\Leftrightarrow\left(\dfrac{2,5\sqrt{3}}{5}\right)^2+\left(\dfrac{x_N}{10}\right)^2=1\Leftrightarrow x_N=\pm2,5\left(cm\right)\)
Tính khoảng cách nên ko cần quan tâm xN dương hay âm
\(MN=\sqrt{ON^2+OM^2}=\sqrt{2,5^2+\left(2,5\sqrt{3}\right)^2}=5cm\)

Đáp án A
Tần số dao động của con lắc lò xo: f = 1 2 π k m không phụ thuộc vào cách treo và biên độ. Do vậy với m và k không đổi, tần số của con lắc không đổi.

Chọn B
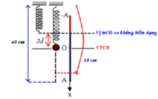
+ Ta có: A = (lmax – lmin) : 2 = 5 (cm) và lcân bằng = (lmax + lmin) : 2 = 35 (cm).
+ Lò xo có chiều dài l = 38 cm > lcân bằng
+ Li độ của chất điểm là: x = 38 – 35 = 3cm = 0,03m.
Mà: F = k.(Δl + x)
ó 10 = 100.(Δl + 0,03)
=> Δl = 0,07m = 7cm.
=> Δlmax = 7 + 5 = 12cm.

Biên độ dao động của con lắc là
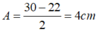
Áp dụng định luật bảo toàn năng lượng ta có
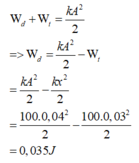
Đáp án D

Ta có: \(\omega=2\pi f=5\pi\) ; A = 4cm
\(\omega=\sqrt{\frac{K}{m}}=\sqrt{\frac{K}{0,1}}\Rightarrow K=25\)
\(\Delta l_o=\frac{mg}{k}=\frac{0,1.10}{25}=4cm\)
Áp dụng CT: \(F_{đh}max=K\left(\Delta l_o+A\right)\) và \(F_{đh}min=k\left(\Delta l_o-A\right)\)
Suy ra, Fmax = 2 N và Fmin = 0 N
Theo mình là đáp án khác.

+ Hai con lắc dao động cùng tần số: f 1 = f 2 ⇒ k m = g l ⇒ m = k l g = 10.0 , 49 9 , 8 = 0 , 5 k g
Chọn đáp án C

Đáp án A
Phương pháp: Động năng của con lắc biến thiên theo thời gian với tần số bằng 2 lần tần số của dao động điều hoà
Cách giải:
Gọi f là tần số dao động của con lắc thì động năng của con lắc biến thiên theo thời gian với tần số 2f
Tần số dao động: f = 1 2 π k m = 1 2 π 36 0 , 1 = 3 Hz
Vậy động năng của con lắc biến thiên theo thời gian với tần số f’ = 2.3 = 6Hz

Chọn đáp án A
Tân số dao đông của con lắc lò xo: f = 1 2 π k m không phụ thuộc vào cách treo và biên độ. Do vậy với m và k không đổi, tần số của con lắc không đổi

Chọn đáp án B
v 2 = ω 2 A 2 − x 2 x 2 = l − l c b 2
⇒ v 2 = g Δ l 0 A 2 − l − l 0 − Δ l 0 2
→ 60 3 2 = g Δ l 0 A 2 − 1 − Δ l 0 2
= g Δ l 0 A 2 − 7 − Δ l 0 2 ⇒ Δ l 0 = 4 c m A = 0 , 6 145 c m
v ¯ = 2 Δ l 0 + A 2 T 2 π arcsin Δ l 0 A + T 4
= 4 + 0.6 145 0 , 4 2 arcsin 4 0 , 6 145 + 0 , 4 4 = 81 , 72 c m / s
10363022