
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b ) \(\Rightarrow\frac{2x}{3}.\frac{1}{12}=\frac{3y}{4}.\frac{1}{12}=\frac{4z}{5}.\frac{1}{12}\)
\(\Rightarrow\frac{x}{18}=\frac{y}{16}=\frac{z}{15}\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{x}{18}=\frac{y}{16}=\frac{z}{15}=\frac{x+y+z}{18+16+15}=\frac{49}{49}=1\)
\(\Rightarrow x=1.18=18\)
\(y=1.16=16\)
\(z=1.15=15\)
Vậy x = 18 ; y = 16 ; z = 15
a ) Từ 3x = 2y ; 2y = 5z \(\Rightarrow\frac{x}{2}=\frac{y}{3};\frac{y}{5}=\frac{z}{2}\)
Ta có :
\(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{10}=\frac{y}{15}\) ( 1 )
\(\frac{y}{5}=\frac{z}{2}\Rightarrow\frac{y}{15}=\frac{z}{6}\) ( 2 )
Do đó : \(\frac{x}{10}=\frac{y}{15}=\frac{z}{6}=\frac{x-y+z}{10-15+6}=\frac{32}{1}=32\)
\(\Rightarrow x=32.10=320\)
\(y=32.15=480\)
\(z=32.6=192\)
Vậy x = 320 ; y = 480 ; z = 192

Gọi giao điểm KD và BE tại I
ta có \(\widehat{DKA}+\widehat{KDA}=90^0\)
\(\widehat{DBI}+\widehat{BDI}=90^0\)
Mà \(\widehat{KDA}=\widehat{BDI}\left(đ.đ\right)\)
=> \(\widehat{DKA}=\widehat{ABI}\)
Ta lại có : góc DKA + góc KDA = Góc ABE+ góc AEB=\(90^0\)
Mà Góc DKA=ABI
=> Góc KDA= Góc AEB
=> tam giác KDA = Tam giác BAE (G.G.G)(tự cm )
=> AK=AB(Cạnh t/u)
mà AB=AC (gt )
=> AK=AC

a)\(A=\frac{4^6.9^5+6^9.120}{-8^4.3^{12}-6^{11}}=\frac{\left(2^2\right)^6+\left(3^2\right)^5+2^9.3^9.2^3.3.5}{-\left(2^3\right)^4.3^{13}-2^{11}.3^{11}}\)
\(=\frac{2^{12}.3^{10}+2^{12}.3^{10}.5}{-2^{12}.3^{12}-2^{11}.3^{11}}=\frac{2^{12}.3^{10}.\left(1+5\right)}{-2^{11}.3^{11}.\left(2.3+1\right)}=\frac{2.6}{-3.7}=-\frac{4}{7}\)
b)\(B=\frac{1}{1-\frac{1}{1-2}}+\frac{1}{1+\frac{1}{1+2^{-1}}}=\frac{1}{1-\frac{1}{-1}}+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}\)
\(=\frac{1}{1+1}+\frac{1}{1+\frac{1}{\frac{3}{2}}}=\frac{1}{2}+\frac{1}{1+\frac{2}{3}}+\frac{1}{2}+\frac{1}{\frac{5}{3}}=\frac{1}{2}+\frac{3}{5}=\frac{11}{10}\)

Bài 3:
Giải:
Gọi số học sinh lớp 7A, 7B, 7C là a, b, c ( a,b,c\(\in\)N* )
Ta có: \(\frac{a}{7}=\frac{b}{8}=\frac{c}{9}\) và a + b - c = 25
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{7}=\frac{b}{8}=\frac{c}{9}=\frac{a+b-c}{7+8-9}=\frac{24}{6}=4\)
+) \(\frac{a}{7}=4\Rightarrow a=28\)
+) \(\frac{b}{8}=4\Rightarrow b=32\)
+) \(\frac{c}{9}=4\Rightarrow c=36\)
Vậy lớp 7A có 28 học sinh
lớp 7B có 32 học sinh
lớp 7C có 36 học sinh

Bài 2
a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
b) Xem hình vẽ:
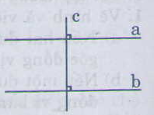
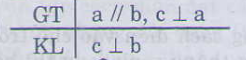 .
.
Bài 4:
Nếu hai đường thẳng cùng vuông góc với đường thẳng thứ 3 thì hai đường thẳng đó song song với nhau:
GT: a vuông góc với c, b vuông góc với c
KL: a song song với b
Bài 3 chịu


Bài 9:
a) Gọi 3 phần cần tìm lần lượt là a,b,c
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}\) = \(\frac{b}{3}\) = \(\frac{c}{5}\) = \(\frac{a+b+c}{2+3+5}\) = \(\frac{6200}{10}\) = 620
\(\Rightarrow\) \(\left[\begin{array}{nghiempt}a=620.2\\b=620.3\\c=620.5\end{array}\right.\) \(\Rightarrow\) \(\left[\begin{array}{nghiempt}a=1240\\b=1860\\c=3100\end{array}\right.\)
Vậy 3 phần cần tìm lần lượt là 1240 ; 1860 ; 3100
b) Gọi 3 phần cần tìm lần lượt là a, b,c
Vì a , b ,c tỉ lệ nghịch với 2 ; 3 ; 5 nên ta có:
a . 2 = b . 3 = c . 5 và a + b + c = 6200
Có: \(\frac{a}{\frac{1}{2}}\) = \(\frac{b}{\frac{1}{3}}\) = \(\frac{c}{\frac{1}{5}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{\frac{1}{2}}\) = \(\frac{b}{\frac{1}{3}}\) = \(\frac{c}{\frac{1}{5}}\) = \(\frac{a+b+c}{\frac{1}{2}+\frac{1}{3}+\frac{1}{5}}\) = \(\frac{6200}{\frac{31}{30}}\) = 6200 . \(\frac{30}{31}\) = 6000
\(\Rightarrow\) \(\left[\begin{array}{nghiempt}a=6000.\frac{1}{2}\\b=6000.\frac{1}{3}\\c=6000.\frac{1}{5}\end{array}\right.\) \(\Rightarrow\) \(\left[\begin{array}{nghiempt}a=3000\\b=2000\\c=1200\end{array}\right.\)
Vậy 3 phần cần tìm lần lượt là 3000 ; 2000 ; 1200
Bài 10.
a) Vì y tỉ lệ tuận với x nên ta có công thức:
y = kx hay 8 = k6
=> k = \(\frac{8}{6}\) = \(\frac{4}{3}\)
Biểu diễn y theo x : y = \(\frac{4}{3}\) . x
b) Khi x = 9 thì y = \(\frac{4}{3}\) . 9 = 12
c) Khi y = - 4:
Ta có: - 4 = \(\frac{4}{3}\) . x
=> x = -4 : \(\frac{4}{3}\) = -4 . \(\frac{-3}{4}\) = -3
Bài 11.
a) Vì x và y tỉ lệ nghịch với nhau nên ta có công thức:
x . y = a hay 4 . (-15) = -60
Biểu diễn y theo x: y = \(\frac{-60}{x}\)
b) Khi x = 6 thì y = \(\frac{-60}{6}\) = -10
Khi x = -12 thì y = \(\frac{-60}{-12}\) = 5
c)
+) Khi y = -2
Ta có công thức: -2 = \(\frac{-60}{x}\)
=> x = \(\frac{-60}{-2}\) = 30
+) Khi y = 30
Tương tự ta có: x = \(\frac{-60}{30}\) = -2





 Giúp mình với nhé
Giúp mình với nhé
 Cac bạn giúp mk nha mai mk thi rồi
Cac bạn giúp mk nha mai mk thi rồi




 mình bài 9,10,11 nhé các bạn thân yêu
mình bài 9,10,11 nhé các bạn thân yêu các bạn giúp mình với mai mình học rồi
các bạn giúp mình với mai mình học rồi
ai trả lời đúng và nhanh nhât sẽ dc 2 tick (phải giải thích). Ko cần làm Câu (7) (8) (9) và a)