
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi thời gian làm 1 mình xong công việc của người thứ nhất là x giờ (x>0)
Thời gian làm 1 mình xong công việc của người 2 là y giờ (y>0)
Trong 1h người thứ nhất làm 1 mình được \(\dfrac{1}{x}\) phần công việc, người 2 làm 1 mình được \(\dfrac{1}{y}\) phần công việc
Do 2 người cùng làm trong 18h thì xong nên:
\(18\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\)
Người thứ nhất làm 4h được: \(\dfrac{4}{x}\) phần công việc
Người thứ 2 làm trong 7h được: \(\dfrac{7}{y}\) phần công việc
Do... trong 7h được 1/3 công việc nên: \(\dfrac{4}{x}+\dfrac{7}{y}=\dfrac{1}{3}\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{4}{x}+\dfrac{7}{y}=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{54}\\\dfrac{1}{y}=\dfrac{1}{27}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=54\\y=27\end{matrix}\right.\)

Nửa chu vi hình chữ nhật:14 cm
Gọi chiều dài hình chữ nhật là x (cm) với \(7< x< 14\)
Chiều rộng hình chữ nhật là: \(14-x\) (cm)
Diện tích ban đầu của hình chữ nhật: \(x\left(14-x\right)\)
Chiều dài hình chữ nhật sau khi tăng 1cm: \(x+1\)
Chiều rộng sau khi tăng 2cm: \(14-x+2=16-x\)
Diện tích lúc sau: \(\left(x+1\right)\left(16-x\right)\)
Do diện tích tăng lên 25 \(cm^2\) nên ta có pt:
\(\left(x+1\right)\left(16-x\right)-x\left(14-x\right)=25\)
\(\Leftrightarrow x+16=25\)
\(\Leftrightarrow x=9\left(cm\right)\)
Vậy hình chữ nhật ban đầu dài 9cm và rộng 5cm


\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...

a: \(=\dfrac{\sqrt{3}\left(x\sqrt{2}+y\sqrt{5}\right)}{2\left(x\sqrt{2}+y\sqrt{5}\right)}=\dfrac{\sqrt{3}}{2}\)
b: \(=\dfrac{a+\sqrt{a}-a-2}{\sqrt{a}+1}:\dfrac{a-\sqrt{a}+\sqrt{a}-4}{a-1}\)
\(=\dfrac{\left(\sqrt{a}-2\right)}{\sqrt{a}+1}\cdot\dfrac{a-1}{a-4}=\dfrac{\sqrt{a}-1}{\sqrt{a}+2}\)

@hieu nguyen Em có nhân chéo hai vế và khai triển ra nhưng cũng không ra cái gì ạ.

a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp




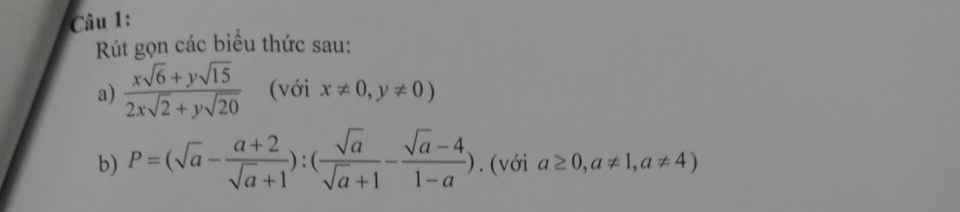

\(A=\left(4x^2+2\cdot2\cdot\dfrac{1}{4}x+\dfrac{1}{16}\right)-\dfrac{1}{16}=\left(2x+\dfrac{1}{4}\right)^2-\dfrac{1}{16}\ge-\dfrac{1}{16}\\ A_{min}=-\dfrac{1}{16}\Leftrightarrow2x+\dfrac{1}{4}=0\Leftrightarrow x=-\dfrac{1}{8}\)
\(A=4x^2+x=\left[\left(2x\right)^2+x+\dfrac{1}{16}\right]-\dfrac{1}{16}=\left(2x+\dfrac{1}{4}\right)^2-\dfrac{1}{16}\ge-\dfrac{1}{16}\)
Dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{8}\)
Vậy \(MinA=-\dfrac{1}{6}\) khi \(x=-\dfrac{1}{8}\)