Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

# Nhập dãy số từ bàn phím
lst = list(map(int, input("Nhập dãy số cách nhau bởi dấu cách: ").split()))
# Sắp xếp dãy số theo thuật toán sắp xếp chọn
for i in range(len(lst)):
min_idx = i
for j in range(i+1, len(lst)):
if lst[j] < lst[min_idx]:
min_idx = j
lst[i], lst[min_idx] = lst[min_idx], lst[i]
# In kết quả ra màn hình
print("Dãy số đã sắp xếp:", lst)

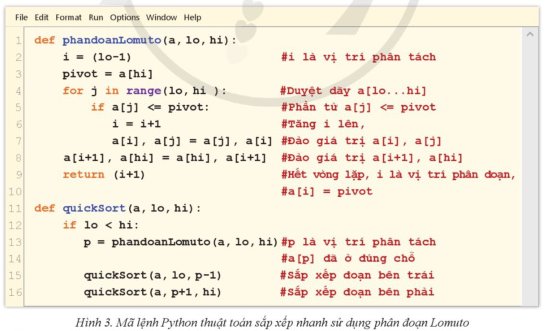
a. Dựa trên mã lệnh thuật toán cho trong Hình 3.

b) Dựa trên mã lệnh thuật toán cho trong Hình 5.


1. Sắp xếp chèn (Insertion Sort)
Ý tưởng: Insertion Sort lấy ý tưởng từ việc chơi bài, dựa theo cách người chơi "chèn" thêm một quân bài mới vào bộ bài đã được sắp xếp trên tay.
2. Sắp xếp lựa chọn (Selection Sort)
Ý tưởng của Selection sort là tìm từng phần tử cho mỗi vị trí của mảng hoán vị A' cần tìm.
3. Sắp xếp nổi bọt (Bubble Sort)
Ý tưởng: Bubble Sort, như cái tên của nó, là thuật toán đẩy phần tử lớn nhất xuống cuối dãy, đồng thời những phần tử có giá trị nhỏ hơn sẽ dịch chuyển dần về đầu dãy. Tựa như sự nổi bọt vậy, những phần tử nhẹ hơn sẽ nổi lên trên và ngược lại, những phần tử lớn hơn sẽ chìm xuống dưới.

*Thuật toán sắp xếp chèn (Insertion Sort):
import time
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp chèn
insertion_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là 0 giây
*Thuật toán sắp xếp chọn:
import time
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp chọn
selection_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là: 0 giây
*Thuật toán sắp xếp nổi bọt:
import time
def bubble_sort(arr):
n = len(arr)
for i in range(n - 1):
for j in range(n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp nổi bọt
bubble_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là: 0 giây

Diễn biến từng bước sắp xếp nhanh một dãy số cụ thể dùng phân đoạn Lomuto sẽ khác với dùng phân đoạn Hoare. Sự khác biệt giữa phương pháp phân đoạn Lomuto và phân đoạn Hoare trong thuật toán QuickSort là ở việc chọn pivot, cách phân đoạn và cách sắp xếp các phần tử.
Cụ thể, phương pháp phân đoạn Lomuto sẽ chọn pivot là phần tử cuối cùng của mảng, phân đoạn theo pivot và sau đó đưa pivot về giữa hai phân đoạn, tiếp tục thực hiện thuật toán QuickSort trên hai phân đoạn trái và phải của pivot. Trong khi đó, phương pháp phân đoạn Hoare sẽ chọn pivot là phần tử ở giữa mảng, đưa hai con trỏ từ đầu và cuối mảng trỏ tới nhau và dịch chuyển chúng sao cho phần tử bên trái pivot lớn hơn pivot, phần tử bên phải pivot nhỏ hơn pivot, sau đó đưa pivot về vị trí mới và thực hiện QuickSort trên hai phân đoạn trái và phải của pivot.

program TrungBinhCong;
const
MAX = 100;
var
danhSach: array[1..MAX] of integer;
n, i, tong: integer;
trungbinh: real;
begin
write('Nhap so ptu (toi da 100): ');
readln(n);
tong := 0;
for i := 1 to n do
begin
write('Nhap giatri ptu thu ', i, ': ');
readln(danhsach[i]);
tong := tong + danhsach[i];
end;
trungbinh := tong / n;
writeln('Tbc cua danh sach la: ', trungbinh:0:2);
readln;
end.
Var a:array[1..100] of integer;
i,n:integer;
s:longint;
tbc:real;
Begin
Repeat
Write('n = ');readln(n);
Until (n>0) and (n<=100);
For i:=1 to n do
Begin
Write('Nhap phan tu thu ',i);readln(a[i]);
s:=s+a[i];
End;
tbc:=s/n;
Write('Trung binh cong la ',tbc:10:2);
Readln
End.

tham khảo!
def nhapDL(finp):
f = open(finp)
A = []
B = []
for line in f:
s = line.split()
A.append(s[0])
temp = s[1:len(s)]
temp = [float(x) for x in temp]
B.append(temp)
f.close()
return A, B
def diem_gk(d):
diem = sum(d) + d[0] + d[len(d) - 1]
diem = diem / (len(d) + 2)
return round(diem, 2)
def xuly(B):
kq = []
for i in range(len(B)):
diem = diem_gk(B[i])
kq.append(diem)
return kq
def ghiDL(fout, A, B):
f = open(fout, "w")
A, B = zip(*sorted(zip(A, B), key=lambda x: x[1], reverse=True))
for i in range(len(A)):
print(A[i], B[i], file=f)
f.close()
finp = "seagames.inp"
fout = "ketqua.out"
DS, Diem = nhapDL(finp)
Kq = xuly(Diem)
ghiDL(fout, DS, Kq)


Câu lệnh in ra màn hình: print(".....")
Các bước thực hiện
- Phân tích bài toán.
- Độ phức tạp thuật toán.