Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tại mặt đất: \(g_0=G\cdot\dfrac{M}{R^2}\)
Tại độ cao h: \(g=G\cdot\dfrac{M}{\left(R+h\right)^2}\)
Xét tỉ lệ:
\(\dfrac{g_0}{g}=\dfrac{\left(R+h\right)^2}{R^2}=\dfrac{9,81}{4,9}=2\)
\(\Rightarrow\dfrac{\left(R+h\right)^2}{R^2}=2\Rightarrow h=2650,97km\)

Ở độ cao khoảng 25,8 m so với mặt đất thì có g=8.9 và vật rơi mất 38 s

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.
F h d = F h t ⇔ G m M r 2 = m v 2 r ⇒ v = G M r
Với: r = R + h = R + R = 2 R
Nên: v = G M 2 R
Mặt khác:
Gia tốc rơi tự do của vật ở mặt đất: g = G M R 2 ⇒ G M = g R 2
⇒ v = g R 2 2 R = g R 2 = 9 , 8.6400000 2 = 5600 m / s = 5 , 6 km / s
Đáp án: D

Chọn đáp án C
+ Gia tốc rơi tự do tại mặt dất:
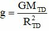
+ Gia tốc rơi tự do tại độ cao h:
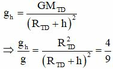
![]()
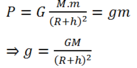
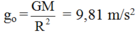
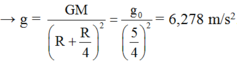
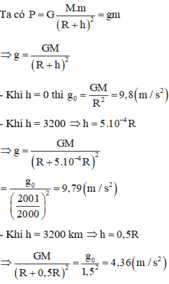
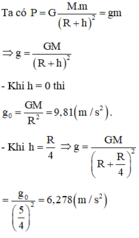
1.
gọi m là trọng lượng vật, M là trọng lượng trái đất
trọng lực của vật bằng lực hấp dẫn trái đất tác dụng lên vật
tại mặt đất \(F_{hd0}=P_0\Leftrightarrow P_0=\dfrac{G.m.M}{R^2}\)
tại vị trí h \(F_{hd}=P\Leftrightarrow P=\dfrac{G.m.M}{\left(R+h\right)^2}\)
lấy P chia P0
\(\Leftrightarrow\dfrac{P}{P_0}=\dfrac{R^2}{\left(R+h\right)^2}\) với h=R
\(\Leftrightarrow\dfrac{P}{600}=\dfrac{1}{4}\Rightarrow P=150N\) (R+h=2R)
2.
gọi m là trọng lượng vật, M là trọng lượng trái đất
\(g_0=\dfrac{G.M}{R^2}\) (1)
gia tốc của vật ở độ cao h1=10000m
\(g=\dfrac{G.M}{\left(R+h_1\right)^2}\) (2)
lấy (2) chia (1)\(\Rightarrow\dfrac{g}{g_0}=\dfrac{R^2}{\left(R+h_1\right)^2}\Rightarrow g\approx9,77\)m/s2
ở độ cao h=\(\dfrac{R}{2}\)
\(g_1=\dfrac{G.M}{\left(R+h\right)^2}\) (3)
lấy (3) chia (1)\(\Rightarrow\dfrac{g_1}{g_0}=\dfrac{R^2}{\left(R+h\right)^2}\Rightarrow\)\(\dfrac{g_1}{g_0}=\dfrac{1}{\left(\dfrac{9}{4}\right)}\)\(\Rightarrow g_1=\)4,36m/s2
3.
như bài 2 nên mình làm tắt
\(\dfrac{g}{g_0}=\dfrac{R^2}{\left(R+h\right)^2}\)\(\dfrac{4,9}{9,8}\)
\(\Rightarrow\dfrac{R}{R+h}=\dfrac{\sqrt{2}}{2}\Rightarrow h=\).........
4.
\(\dfrac{P}{P_0}=\dfrac{R^2}{\left(R+h\right)^2}=\dfrac{50}{450}\Rightarrow\dfrac{R}{R+h}=\dfrac{1}{3}\Rightarrow h=2R\)