Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


CÓ:
Xét \(\Delta\)AEC có: \(\widehat{ACE}=180^o-\widehat{AEC}-\widehat{EAC}\)
Xét \(\Delta\)ADB có: \(\widehat{ABD}=180^o-\widehat{ADB}-\widehat{DAB}\)
Mà \(\widehat{AEC}=\widehat{ADB}\left(gt\right);\widehat{EAC}=\widehat{DAB}\left(=\widehat{BAC}\right)\)
=> \(\widehat{ACE}=\widehat{ABD}\)
=> \(2.\widehat{ACE}=2.\widehat{ABD}\)
=> \(\widehat{ABC}=\widehat{ACB}.\)

a)(x - 1) x + 2 = (x - 1)x + 4
=> (x - 1) x + 4 - (x - 1)x + 2 = 0
=> (x - 1)x + 2 . [(x - 1)2 - 1] = 0
=> \(\orbr{\begin{cases}\left(x-1\right)^{x+2}=0\\\left(x-1\right)^2-1=0\end{cases}\Rightarrow\orbr{\begin{cases}\left(x-1\right)^{x+2}=0^{x+2}\\\left(x-1\right)^2=1^2\end{cases}\Rightarrow}\orbr{\begin{cases}x-1=0\\x-1=\pm1\end{cases}}}\)
Nếu x - 1 = 0
=> x = 1
Nếu x - 1 = - 1
=> x = 0
Nếu x - 1 = 1
=> x = 2
Vậy \(x\in\left\{0;1;2\right\}\)
b) \(\left(1,78^{2x-2}-1,78^x\right):1,78^x=0\)
\(\Rightarrow1,78^{2x-2}:1,78^x-1,78^x:1,78^x=0\)
\(\Rightarrow1,78^{x-2}-1=0\)
\(\Rightarrow1,78^{x-2}=1\)
\(\Rightarrow1,78^{x-2}=1,78^0\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=2\)
Vậy x = 2

f(2015)=a(2015)^5+b(2015)^3+2014.2015 +1 mà f(2015)=2 => a(2015)^5+b(2015)^3+2014.2015+1=2 =>a(2015)^5+b(2015)^3+2014.2015 =1
Xét f(-2015)=a(-2015)^5+b(-2015)^3+2014.(-2015) +1=-a(2015)^5-b(2015)^3-2014.2015 +1 = -(a(2015)^5+b(2015)^3+2014.2015)+1 =-1+1=0
bài dễ
ta có f(2015)=a.2015^5+b.2015^3+2014.2015+1
f(-2015)=a.(-2015)^5+b.(-2015)^3+2014.(-2015)+1
=>f(2015)+f(-2015)=2
(=)2+f(-2015)+2
(=) f(-2015)=0

Bài 1:
x y m B A C 1 1 2 1
Qua B, vẽ tia Bm sao cho Bm // Ax
Bm // Ax ( cách vẽ ) => góc A1 + góc B1 = 180o ( trong cùng phía )
Mà góc A1 = 140o ( giả thiết ) => góc B1 = 40o
Ta có: góc B1 + góc B2 = góc ABC
Mà góc ABC = 70o ( giả thiết ); góc B1 = 40o ( chứng minh trên )
=> góc B2 = 30o
Ta có: góc B2 + góc C1 = 30o + 150o = 180o
Mà hai góc này ở vị trí trong cùng phía
=> Bm // Cy ( dấu hiệu nhận biết 2 đường thẳng song song )
Ta lại có:
Ax // Bm ( cách vẽ ); Cy // Bm ( chứng minh trên )
=> Ax // Cy ( tính chất 3 quan hệ từ vuông góc đến song song ) ( đpcm )
Bài 3:
A B C F E G N M H 1 2
a) Chứng minh AH < \(\dfrac{1}{2}\) ( AB + AC )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AB ( quan hệ giữa đường vuông góc và đường xiên ) ( 1 )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AC ( quan hệ giữa đường vuông góc và đường xiên ) ( 2 )
+) Từ ( 1 ) và ( 2 ) => AH + AH < AB + AC
=> 2 . AH < AB + AC
=> AH < \(\dfrac{1}{2}\) ( AB + AC ) ( đpcm )
b) Chứng minh EF = BC
+) Vì BM là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{BG}{BM}=\dfrac{2}{3}\)
=> \(\dfrac{MG}{BG}=\dfrac{1}{2}\)
=> 2 . MG = BG
Mà EM = MG ( do BM là đường trung tuyến của tam giác ABC )
=> EM + MG = BG => EG = BG
+) Vì CN là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{CG}{CN}=\dfrac{2}{3}\)
=> \(\dfrac{GN}{CG}=\dfrac{1}{2}\)
=> 2 . GN = CG
Mà FN = GN ( do CN là đường trung tuyến của tam giác ABC )
=> FN + GN = CG => FG = CG
Góc G1 = góc G2 ( đối đỉnh )
Xét tam giác FEG và tam giác CBG có:
FG = CG ( chứng minh trên )
EG = BG ( chứng minh trên )
Góc G1 = góc G2 ( chứng minh trên )
=> tam giác FEG = tam giác CBG ( c.g.c )
=> EF = BC ( 2 cạnh tương ứng ) ( đpcm )


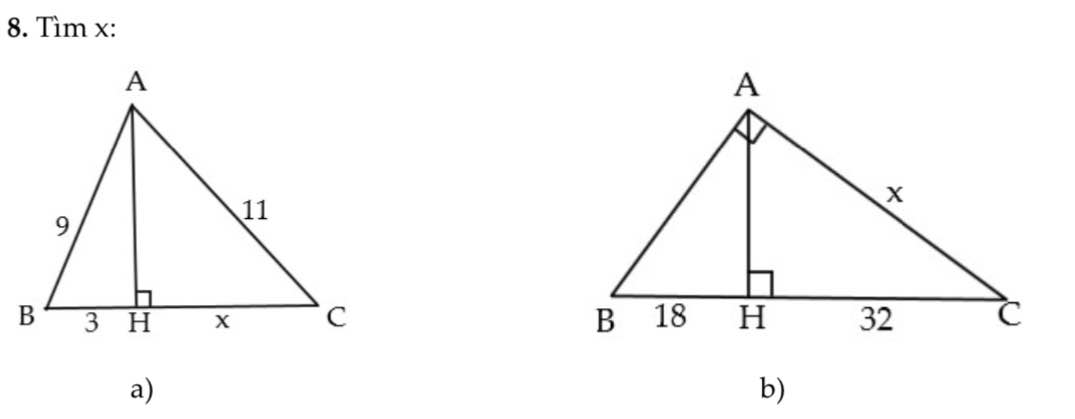
a, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH}=\sqrt{81-9}=6\sqrt{2}\)
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=x=\sqrt{AC^2-AH^2}=7\)
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=1600\Rightarrow AC=x=40\)

Bài 1:
Mình có hình cho câu a) thôi nha.
a) Xét 2 \(\Delta\) \(ABD\) và \(ACD\) có:
\(AB=AC\left(gt\right)\)
\(BD=CD\) (vì D là trung điểm của \(BC\))
Cạnh AD chung
=> \(\Delta ABD=\Delta ACD\left(c-c-c\right)\)
=> \(\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng).
=> \(AD\) là tia phân giác của \(\widehat{BAC}.\)
b) Vì \(\widehat{BAD}=\widehat{CAD}\left(cmt\right)\)
=> \(\widehat{MAD}=\widehat{NAD}.\)
Xét 2 \(\Delta\) \(AMD\) và \(AND\) có:
\(AM=AN\left(gt\right)\)
\(\widehat{MAD}=\widehat{NAD}\left(cmt\right)\)
Cạnh AD chung
=> \(\Delta AMD=\Delta AND\left(c-g-c\right)\)
=> \(\widehat{AMD}=\widehat{AND}\) (2 góc tương ứng).
Mà \(\widehat{AMD}=90^0\left(gt\right)\)
=> \(\widehat{AND}=90^0.\)
=> \(DN\perp AN\)
Hay \(DN\perp AC.\)
Chúc bạn học tốt!
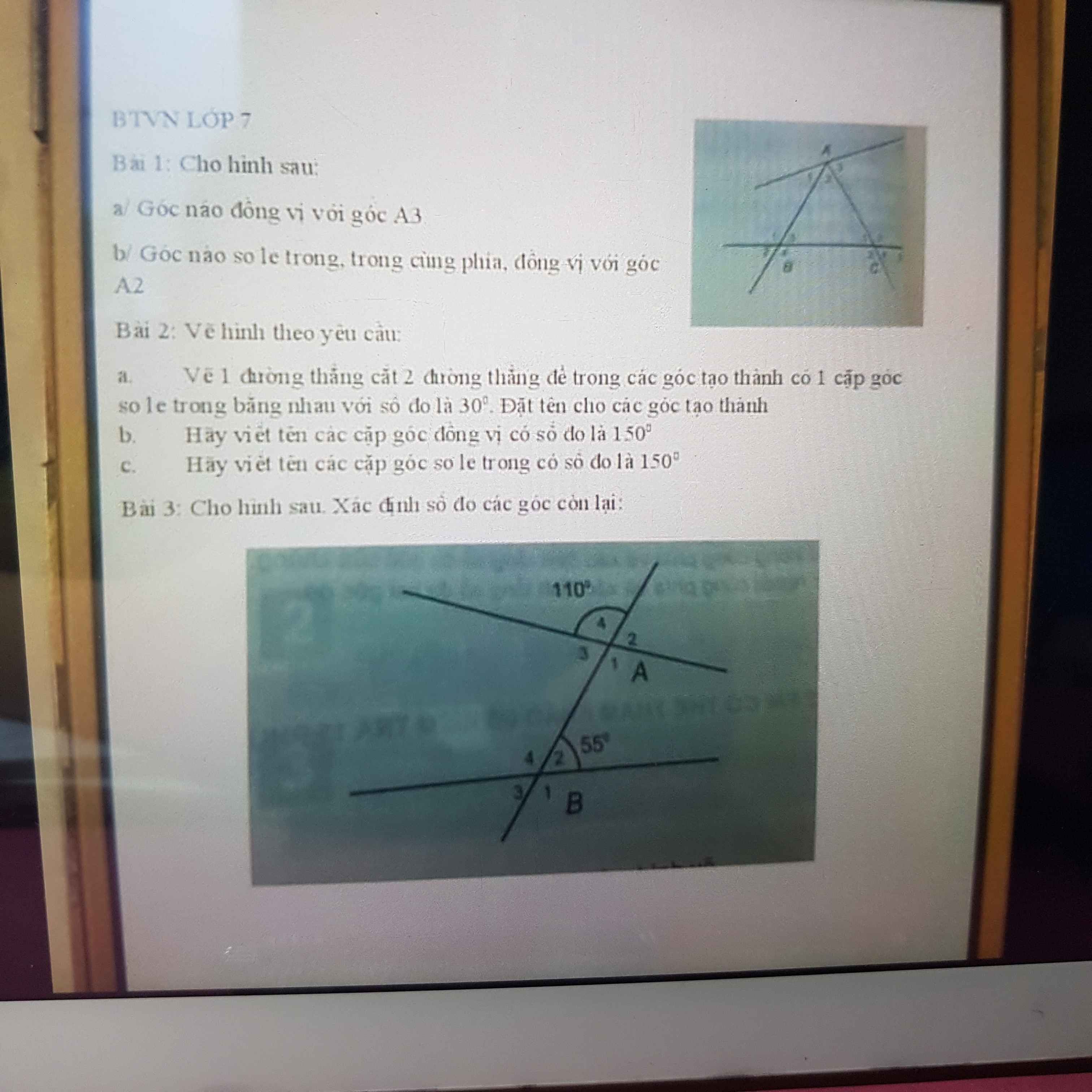



bn đánh bài tập 2 ra hộ mik với chứ để ảnh khó nhìn lém
Bài 3:
\(\widehat{A_1}=110^0;\widehat{A_2}=70^0;\widehat{A_3}=70^0\)
\(\widehat{B_3}=55^0;\widehat{B_4}=125^0;\widehat{B_1}=125^0\)