Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(\frac{\text{P}_đ}{\text{P}_{\text{h}}}=\frac{\text{mg}_đ}{\text{mg}_{\text{h}}}=\frac{\text{g}_đ}{\text{g}_{\text{h}}}=\frac{\text{GM}\div\text{R}^2}{\text{GM}\div\left(\text{R}+\text{h}\right)^2}=\left(\frac{\text{R}+\text{h}}{\text{R}}\right)^2\)
\(\Rightarrow\frac{20}{10}=\left(\frac{6400+\text{h}}{6400}\right)^2\)
\(\Rightarrow\sqrt{2}=\frac{6400+\text{h}}{6400}\)
\(\Rightarrow\text{h}=2651\text{ km}\)

Lực hút của trái đất là lực hấp dẫn giữa trái đất và vật.
\(F_{hd}=G.\dfrac{mM}{(R+h)^2}\)
Ở mặt đất: \(F_1=G.\dfrac{mM}{R^2}\)
Ở độ cao h: \(F_2=G.\dfrac{mM}{(R+h)^2}\)
\(\Rightarrow \dfrac{F_1}{F_2}=(\dfrac{R+h}{R})^2=9\)
\(\Rightarrow \dfrac{R+h}{R}=3\)
\(\Rightarrow h = 2.R=2.6400=12800 km\)

\(\dfrac{P}{P_0}=\dfrac{R^2}{\left(R+h\right)^2}\)
P0=9P
\(\Rightarrow\dfrac{1}{3}=\dfrac{R}{R+h}\)
\(\Rightarrow h=2R\)

1/
Trọng lực ở đây đóng vai trò như 1 lực hấp dẫn
Theo đề ta có trọng lượng của quả cầu ở độ cao h bằng 1/4 trọng lượng của nó trên mặt đất
\(P'=\dfrac{1}{4}\cdot P\Rightarrow G\cdot\dfrac{mM}{\left(R+h\right)^2}=\dfrac{1}{4}\cdot G\cdot\dfrac{mM}{R^2}\)
\(\Rightarrow\dfrac{1}{\left(6400\cdot1000+h\right)^2}=\dfrac{1}{4\cdot\left(6400\cdot1000\right)^2}\Rightarrow h=6400000\left(m\right)=6400\left(km\right)\)
ChọnC
2/
Theo đề ta có gia tốc rơi tự do có giá trị bằng 1/3 gia tốc rơi tự do ở mặt đất ở độ cao
\(g'=\dfrac{1}{3}g\Rightarrow G\dfrac{M}{\left(R+h\right)^2}=\dfrac{1}{3}\cdot G\dfrac{M}{R^2}\)
\(\Rightarrow\dfrac{1}{\left(6400\cdot1000+h\right)^2}=\dfrac{1}{3\cdot\left(6400\cdot1000\right)^2}\Rightarrow h=4685125,168\left(m\right)\approx4685\left(km\right)\)
Chọn B

Chọn đáp án B
+ Gia tốc rơi tự do ở độ cao h: 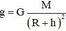
+ Gia tốc rơi tự do ở mặt đất:
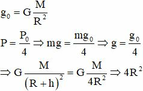
![]()
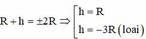
![]()

\(\dfrac{P}{P'}=\dfrac{G\cdot\dfrac{M\cdot m}{R^2}}{G\cdot\dfrac{M\cdot m}{\left(R+h\right)^2}}=\dfrac{\dfrac{1}{R^2}}{\dfrac{1}{\left(R+0,5R\right)^2}}=\dfrac{9}{4}\)
\(\Rightarrow P'=\dfrac{P\cdot4}{9}=\dfrac{45\cdot4}{9}=20\left(N\right)\)
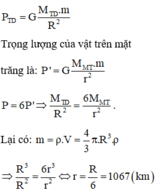
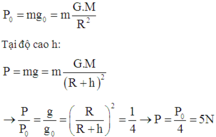
Ta có :
\(\frac{P_h}{P_đ}=\frac{g_h}{g_đ}=\left(\frac{R}{R+h}\right)^2\)
\(\Rightarrow\frac{1}{9}=\left(\frac{R}{R+h}\right)^2\)
\(\Rightarrow\frac{1}{3}=\frac{R}{R+h}\)
\(\Rightarrow h=2R=6400\cdot2=12800\left(\text{km}\right)\)