Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S : quãng đường
V1 : vận tốc đi bộ
V2 : vận tốc đi xe đạp
Ta có S = \(\frac{50}{60}\). V1 = 0.3* V2 => \(\frac{50}{60}\). V1 - 0.3* V2 = 0
Và V2 - V1 = 8
Giải hệ phương trình trên
=> V1 =
V2 =

Lời giải:
Đổi $2$ phút = $\frac{1}{30}$ giờ
Giả sử Hoa dự định đi nửa quãng đường sau với thời gian $a$ giờ thì thực tế Hoa đi nửa quãng đường sau với thời gian là $a-\frac{1}{30}$ (giờ)
Độ dài nửa quãng đường sau là:
$12a=15(a-\frac{1}{30})\Rightarrow a=\frac{1}{6}$ (giờ)
Độ dài nửa quãng đường: $12a=12.\frac{1}{6}=2$ (km)
Độ dài quãng đường từ nhà đến trường là: $2.2=4$ (km)

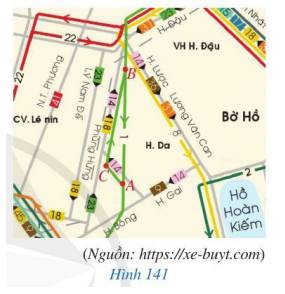
Xét tam giác ABC có: \(AC + CB > AB\).
Vậy nên bạn Hoa đi đường thứ nhất đi từ A đến C và đi tiếp từ C đến B sẽ dài hơn đi đường thứ hai đi từ B đến A.

Bạn An đi đường đi thứ nhất là đường đi thẳng từ nhà đến trường sẽ gần hơn đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường.
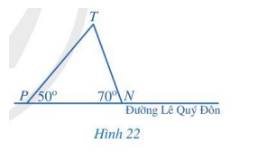

Ta thấy: \(\widehat P < \widehat N\)(50° < 70°) nên NT (cạnh đối diện với góc P) < PT (cạnh đối diện với góc N) (Cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Do đó, bạn Hoa nên xuống ở điểm dừng N rồi đi bộ đến trường.