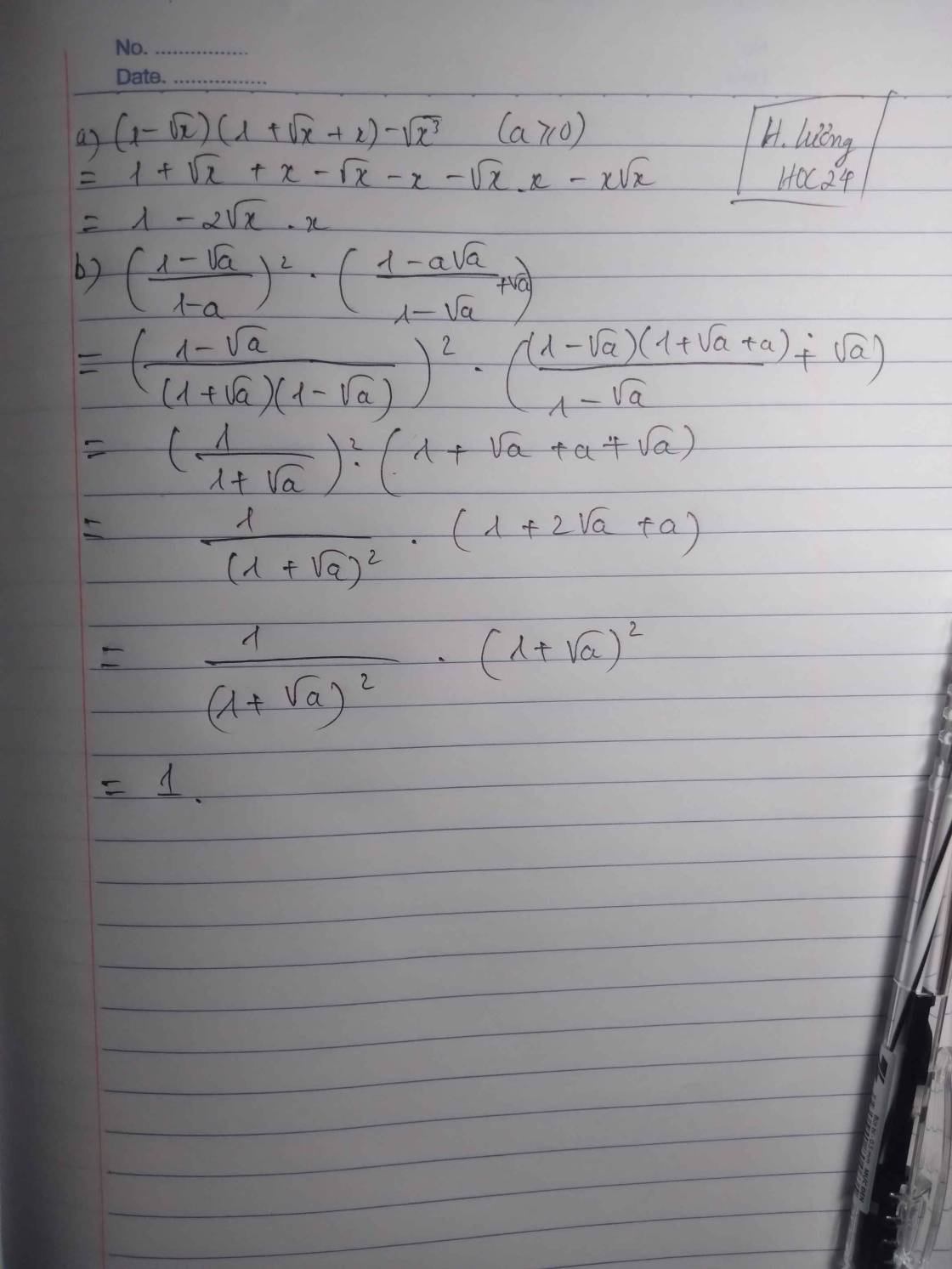Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
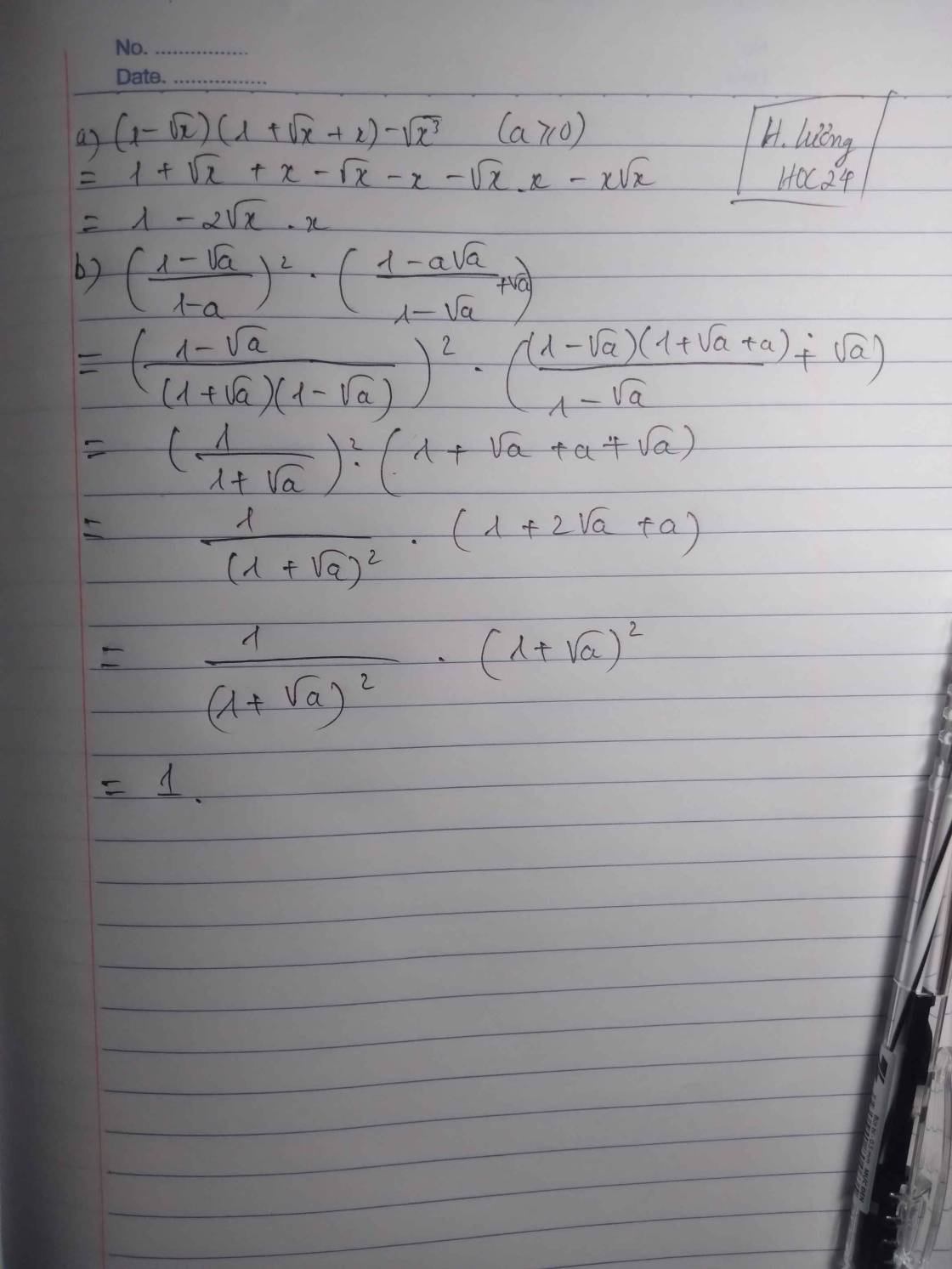chúc bạn học tốt nha
Bài 2:
a: =>25x=35^2=1225
=>x=49
b: \(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+\dfrac{4}{3}\cdot3\sqrt{x+5}=6\)
\(\Leftrightarrow3\sqrt{x+5}=6\)
=>x+5=4
=>x=-1
Biến đổi vế trái ta có:
\(a^3+b^3+c^3=\left(a+b\right)^3-3ab\left(a+b\right)+c^3\)
\(=\left(a+b+c\right)^3-3\left(a+b\right)c\left(a+b+c\right)-3ab\left(a+b\right)\)
\(=\left(a+b+c\right)^3-3\left(a+b\right)\left(ac+bc+c^2+ab\right)\)
\(=\left(a+b+c\right)^3-3\left(a+b\right)\left(a+c\right)\left(b+c\right)\)*
Vì \(a+b+c=0\)\(\Rightarrow\)*\(=-3\left(a+b\right)\left(a+c\right)\left(b+c\right)\)
cũng có \(\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\) Thay vào biểu thức trên ta được
\(-3\left(a+b\right)\left(b+c\right)\left(c+a\right)=3abc\)
\(VT=VP\)=> đpcm
vì \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\Rightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\)
ta có \(B=\dfrac{xyz}{x^3}+\dfrac{xyz}{y^3}+\dfrac{xyz}{z^3}=xyz\left(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}\right)\)
mà \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\Rightarrow B=xyz.\dfrac{3}{xyz}=3\)
\(a)A=\dfrac{\sqrt{3}-\sqrt{6}}{1-\sqrt{2}}-\dfrac{2+\sqrt{8}}{1+\sqrt{2}}\\ A=\dfrac{\left(\sqrt{3}-\sqrt{6}\right)\left(1+\sqrt{2}\right)}{1^2-\left(\sqrt{2}\right)^2}-\dfrac{\left(2+\sqrt{8}\right)\left(1-\sqrt{2}\right)}{1^2-\left(\sqrt{2}\right)^2}\\ A=-\left(\sqrt{3}+\sqrt{6}-\sqrt{6}-2\sqrt{3}\right)+2-2\sqrt{2}+2\sqrt{2}-4\\ A=\sqrt{3}-2\)
\(b)B=\left(\dfrac{1}{x-4}-\dfrac{1}{x+4\sqrt{x}+4}\right).\dfrac{x+2\sqrt{x}}{\sqrt{x}}\\ B=\left[\dfrac{1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{1}{\left(\sqrt{x}+2\right)^2}\right].\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}}\\ B=\dfrac{\sqrt{x}+2-\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)^2}.\left(\sqrt{x}+2\right)\\ B=\dfrac{\sqrt{x}+2-\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}.\left(\sqrt{x}+2\right)\\ B=\dfrac{4}{x-4}\)
a: \(M=\dfrac{x+6\sqrt{x}-3\sqrt{x}+18-x}{x-36}\)
\(=\dfrac{3\left(\sqrt{x}+6\right)}{x-36}=\dfrac{3}{\sqrt{x}-6}\)
b: \(N=\dfrac{x^2}{y}\cdot\sqrt{xy\cdot\dfrac{y}{x}}-x^2\)
\(=\dfrac{x^2}{y}\cdot y-x^2=0\)
a, ĐKXĐ : \(\left[{}\begin{matrix}x\ge0\\ y>0\end{matrix}\right.\) hoặc \(\left[{}\begin{matrix}x>0\\y\ge0\end{matrix}\right.\)
Ta có :\(\frac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2\)
= \(\frac{\sqrt{x^2}\sqrt{x}+\sqrt{y^2}\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2=\frac{\sqrt{x^3}+\sqrt{y^3}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2\)
= \(\frac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-\left(x-2\sqrt{xy}+y\right)\)
= \(\left(x-\sqrt{xy}+y\right)-\left(x-2\sqrt{xy}+y\right)\)
= \(x-\sqrt{xy}+y-x+2\sqrt{xy}-y\)
= \(\sqrt{xy}\)
\(\sqrt{\frac{\sqrt{a}-1}{\sqrt{b}+1}}:\sqrt{\frac{\sqrt{b}-1}{\sqrt{a}+1}}\) \(=\sqrt{\frac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{b}+1\right)\left(\sqrt{b}-1\right)}}\)\(=\sqrt{\frac{a^2-1}{b^2-1}}\) (*)
Thay a=7,25 và b= 3,25 vào (*) ta có:
\(\sqrt{\frac{7,25^2-1}{3,25^2-1}}\) \(=\frac{5\sqrt{33}}{4}:\frac{3\sqrt{17}}{4}=\frac{5\sqrt{33}}{3\sqrt{17}}=\frac{5\sqrt{561}}{51}\)
1: Khi x=64 thì \(A=\dfrac{8+2}{8}=\dfrac{5}{4}\)
2: \(B=\dfrac{x-1+2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
1/ Rút gọn: \(a)3\sqrt{2a}-\sqrt{18a^3}+4\sqrt{\dfrac{a}{2}}-\dfrac{1}{4}\sqrt{128a}\left(a\ge0\right)=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-2\sqrt{2a}=3\sqrt{2a}\left(1-a\right)\)b)\(\dfrac{\sqrt{2}-1}{\sqrt{2}+2}-\dfrac{2}{2+\sqrt{2}}+\dfrac{\sqrt{2}+1}{\sqrt{2}}=\dfrac{\sqrt{2}-1-2}{\sqrt{2}+2}+\dfrac{\sqrt{2}+1}{\sqrt{2}}=\dfrac{\sqrt{2}-3}{\sqrt{2}+2}+\dfrac{\sqrt{2}+1}{\sqrt{2}}=\dfrac{\sqrt{2}-3+2+1+2\sqrt{2}}{\sqrt{2}\left(1+\sqrt{2}\right)}=\dfrac{3\sqrt{2}}{\sqrt{2}\left(1+\sqrt{2}\right)}=\dfrac{3}{1+\sqrt{2}}\)c)\(\dfrac{2+\sqrt{5}}{\sqrt{2}+\sqrt{3+\sqrt{5}}}+\dfrac{2-\sqrt{5}}{\sqrt{2}-\sqrt{3-\sqrt{5}}}=\dfrac{\sqrt{2}\left(2+\sqrt{5}\right)}{\left(\sqrt{2}+\sqrt{3+\sqrt{5}}\right)\sqrt{2}}+\dfrac{\sqrt{2}\left(2-\sqrt{5}\right)}{\sqrt{2}\left(\sqrt{2}-\sqrt{3-\sqrt{5}}\right)}=\dfrac{2\sqrt{2}+\sqrt{10}}{2+\sqrt{6+2\sqrt{5}}}+\dfrac{2\sqrt{2}-\sqrt{10}}{2-\sqrt{6-2\sqrt{5}}}=\dfrac{2\sqrt{2}+\sqrt{10}}{2+\sqrt{\left(\sqrt{5}+1\right)^2}}+\dfrac{2\sqrt{2}-\sqrt{10}}{2-\sqrt{\left(\sqrt{5}-1\right)^2}}=\dfrac{\sqrt{2}\left(2+\sqrt{5}\right)}{2+\sqrt{5}+1}+\dfrac{\sqrt{2}\left(2-\sqrt{5}\right)}{2-\sqrt{5}+1}=\dfrac{\sqrt{2}\left(2+\sqrt{5}\right)}{3+\sqrt{5}}+\dfrac{\sqrt{2}\left(2-\sqrt{5}\right)}{3-\sqrt{5}}=\dfrac{\sqrt{2}\left(2+\sqrt{5}\right)\left(3-\sqrt{5}\right)+\sqrt{2}\left(2-\sqrt{5}\right)\left(3+\sqrt{5}\right)}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}=\dfrac{\sqrt{2}\left(6-2\sqrt{5}+3\sqrt{5}-5+6+2\sqrt{5}-3\sqrt{5}-5\right)}{9-5}=\dfrac{2\sqrt{2}}{4}=\dfrac{1}{\sqrt{2}}\)
Làm nốt nè :3
\(2.a.P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x}=\dfrac{x-1}{x}\left(x>0;x\ne1\right)\)\(b.P>\dfrac{1}{2}\Leftrightarrow\dfrac{x-1}{x}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{x-2}{2x}>0\)
\(\Leftrightarrow x-2>0\left(do:x>0\right)\)
\(\Leftrightarrow x>2\)
\(3.a.A=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{a-\sqrt{a}}\right):\dfrac{\sqrt{a}+1}{a-1}=\dfrac{\sqrt{a}-1}{\sqrt{a}-1}.\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}=\sqrt{a}-1\left(a>0;a\ne1\right)\)
\(b.Để:A< 0\Leftrightarrow\sqrt{a}-1< 0\Leftrightarrow a< 1\)
Kết hợp với DKXĐ : \(0< a< 1\)
Bài 6:
a: \(\Leftrightarrow\sqrt{x^2+4}=\sqrt{12}\)
=>x^2+4=12
=>x^2=8
=>\(x=\pm2\sqrt{2}\)
b: \(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)
=>x+1=1
=>x=0
c: \(\Leftrightarrow3\sqrt{2x}+10\sqrt{2x}-3\sqrt{2x}-20=0\)
=>\(\sqrt{2x}=2\)
=>2x=4
=>x=2
d: \(\Leftrightarrow2\left|x+2\right|=8\)
=>x+2=4 hoặcx+2=-4
=>x=-6 hoặc x=2
