Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A

a) M là trung điểm AC(gt) => AM=CM
Xét tg BMC và tg DMA ta có:
- BM=DM(gt)
- ^BMC=^DMA(đối đỉnh)
- MC=MA(cmt)
=> tg BMC=tg DMA(c.g.c)
b) tg BMC=tg DMA(câu a)
=> ^MBC=^MDA (2 góc tương ứng)
Mà 2 góc này so le trong => AD//BC
Lại có: AH vuông góc BC(gt)
=> AH vuông góc AD (quan hệ //, vuông góc)
c) Ta có: AH vuông góc AD( câu b)
CK vuông góc AD(gt)
=> AH//CK(1)
Mà AD//BC(câu b) hay AK//CH (2)
Từ (1),(2) => AH=CK; AK=CH(3)
Tg BMC= tg DMA (câu a) => BC=DA(4)
Lại có: BC=CH + BH(5)
DA= AK + DK(6)
Từ (3)(4)(5)(6) => BH=DK
Có: ^MBC=^MDA(câu b) hay ^MBH=^MDK
Xét tg BMH và tg DMK có:
- BM=DM(gt)
- ^MBH=^MDK (cmt)
- BH=DK (cmt)
=> tg BMH=tg DMK (c.g.c)
=> ^BMH=^DMK
=>^BMH + ^BMK =^DMK+^BMK
Hay: ^HMK=^BMD=180°
=> H, M, K thẳng hàng

Bài 3:
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra:AC//BD và AC=BD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{CDB}=90^0\)

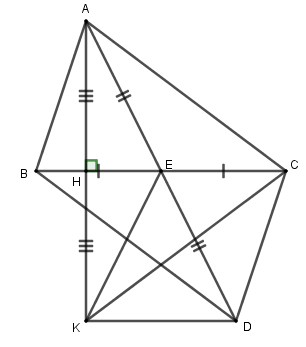
hình bạn nhé :
Xét ΔABEΔABE và ΔDCEΔDCE có :
EB=ECEB=EC (EE là trung điểm BCBC)
EA=EDEA=ED (EE là trung điểm ADAD)
∠AEB=∠DEC∠AEB=∠DEC (đối đỉnh)
⇒ΔABE=ΔDCE(c−g−c)⇒ΔABE=ΔDCE(c−g−c)
b) Chứng minh: AC//BDAC//BD.
Xét ΔACEΔACE và ΔDBEΔDBE có :
EB=ECEB=EC (EE là trung điểm BCBC)
EA=EDEA=ED (EE là trung điểm ADAD)
∠AEC=∠DEB∠AEC=∠DEB (đối đỉnh)
⇒ΔACE=ΔDBE(c−g−c)⇒ΔACE=ΔDBE(c−g−c)
⇒∠ACE=DBE⇒∠ACE=DBE (góc tương ứng)
Mà hai góc ở vị trí so le trong nên AC//BDAC//BD (đpcm)
c) Vẽ AHAH vuông góc với ECEC (HH thuộc BCBC). Trên tia AHAH lấy điểm KK sao cho HH là trung điểm của AKAK. Chứng minh rằng BD=AC=CKBD=AC=CK.
Ta có : ΔACE=ΔDBE(cmt)ΔACE=ΔDBE(cmt)⇒BD=AC⇒BD=AC (cạnh tương ứng) (1)
Xét ΔCAHΔCAH và ΔCKHΔCKH có :
CHCH chung
∠CHA=∠CHK=900∠CHA=∠CHK=900
HA=HK(gt)HA=HK(gt)
⇒ΔCAH=ΔCKH(c−g−c)⇒ΔCAH=ΔCKH(c−g−c)
⇒CA=CK⇒CA=CK (2)
Từ (1) và (2) suy ra AC=BD=CKAC=BD=CK (đpcm)
d) Chứng minh DKDK vuông góc với AHAH.
Nối EE với KK.
Xét ΔEAHΔEAH và ΔEKHΔEKH có :
EHEH chung
∠EHA=∠EHK=900∠EHA=∠EHK=900
HA=HK(gt)HA=HK(gt)
⇒ΔEAH=ΔEKH(c−g−c)⇒ΔEAH=ΔEKH(c−g−c) ⇒∠EAH=∠EKH⇒∠EAH=∠EKH (góc t/ư) (3)
EK=EAEK=EA (cạnh t/ư), mà EA=ED(gt)EA=ED(gt) ⇒EK=ED⇒EK=ED ⇒ΔEKD⇒ΔEKD cân tại EE
⇒∠EKD=∠EDK⇒∠EKD=∠EDK (t/c) (4)
Từ (3) và (4) suy ra ∠EAK+∠EDK=∠EKA+∠EKD=∠AKD∠EAK+∠EDK=∠EKA+∠EKD=∠AKD
Tam giác AKDAKD có : ∠EAK+∠EDK+∠AKD=1800∠EAK+∠EDK+∠AKD=1800
⇒∠AKD+∠AKD=1800⇒2∠AKD=1800⇒∠AKD=1800:2=900⇒∠AKD+∠AKD=1800⇒2∠AKD=1800⇒∠AKD=1800:2=900
Vậy AK⊥KDAK⊥KD (đpcm).
chúc bạn học tốt

A B C I M D H K
a) Xét \(\Delta AIB\),\(\Delta AIC\) có: ^BAI=^CAI (gt) , AI chung, AB=AC
=>\(\Delta AIB\)=\(\Delta AIC\)(c.g.c)
b) Xét\(\Delta AMD\), \(\Delta CMB\) có: ^AMD=^BMC (2 goc đối điỉnh)
AM=MC(gt) ; BM=MD(gt)
=>\(\Delta AMD\)=\(\Delta CMB\)(c.g.c)
=> AD=BC ; BD=AC
Xét \(\Delta ABC\) => AB+BC>AC ( bđt trong tam giác)
mà AC=BD => AB+BC>BD
c) xét \(\Delta AHM\),\(\Delta CKM\) (^AHM=^CKM=90o) có: AM=MC(gt) , ^AMH=^CMK ( 2gocs dd)
=>\(\Delta AHM\)=\(\Delta CKM\)
=>AH=CK
=>AH+CK=2AH
Xét \(\Delta AHM\) vuông tại H:=> ^AMH< ^AHM
=> AM>AH
=>2AM>2AH
mà 2AM=AC(gt) 2AH= AH +CK
=>AC>AH+CK

có bài toán nào hay không cho mình với
có đấy Trần Văn Quàng