Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a, \(C_nH_{2n}+Br_2\rightarrow C_nH_{2n}Br_2\)
\(C_nH_{2n}+\dfrac{3n}{2}O_2\underrightarrow{t^o}nCO_2+nH_2O\)
\(C_3H_8+5O_2\underrightarrow{t^o}3CO_2+4H_2O\)
b, Gọi: \(\left\{{}\begin{matrix}n_{C_nH_{2n}}=x\left(mol\right)\\n_{C_3H_8}=y\left(mol\right)\end{matrix}\right.\) \(\Rightarrow x+y=\dfrac{15,68}{22,4}=0,7\left(1\right)\)
Có: \(n_{CO_2}=n.n_{C_nH_{2n}}+3n_{C_3H_8}=nx+3y=\dfrac{40,32}{22,4}=1,8\left(2\right)\)
Mà: m bình tăng = 16,8 (g) = mCnH2n = 14nx (3)
Từ (1), (2) và (3) \(\Rightarrow\left\{{}\begin{matrix}nx=1,2\\x=0,5\left(mol\right)\\y=0,2\left(mol\right)\end{matrix}\right.\)
⇒ n = 1,2:0,5 = 2,4
Mà: 2 anken đồng đẳng kế tiếp.
→ C2H4 và C3H6.
Có: \(\left\{{}\begin{matrix}28n_{C_2H_4}+42n_{C_3H_6}=16,8\\n_{C_2H_4}+n_{C_3H_6}=0,7-0,2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_4}=0,3\left(mol\right)\\n_{C_3H_6}=0,2\left(mol\right)\end{matrix}\right.\)
%n cũng là %V ở cùng điều kiện nhiệt độ, áp suất.
\(\Rightarrow\left\{{}\begin{matrix}\%V_{C_2H_4}=\dfrac{0,3}{0,7}.100\%\approx42,86\%\\\%V_{C_3H_6}=\%V_{C_3H_8}=\dfrac{0,2}{0,7}.100\%\approx28,57\%\end{matrix}\right.\)
Bài 2:
a, \(n_{CO_2}=\dfrac{13,44}{22,4}=0,6\left(mol\right)\)
\(n_{H_2O}=\dfrac{6,48}{18}=0,36\left(mol\right)\)
\(\Rightarrow n_X=0,6-0,35=0,24\left(mol\right)\)
\(\Rightarrow\overline{C}=\dfrac{0,6}{0,24}=2,5\)
Mà: 2 ankin hơn kém nhau 2 C và số C nhỏ nhất có thể có là 2.
→ C2H2 và C4H6.
CTCT: C2H2: \(CH\equiv CH\)
C4H6: \(CH\equiv C-CH_2-CH_3\) hoặc \(CH_3-C\equiv C-CH_3\)
b, BTNT C, có: \(2n_{C_2H_2}+4n_{C_4H_6}=n_{CO_2}=0,6\left(1\right)\)
BTNT H, có: \(2n_{C_2H_2}+6n_{C_4H_6}=2n_{H_2O}=0,36.2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_2}=0,18\left(mol\right)\\n_{C_4H_6}=0,06\left(mol\right)\end{matrix}\right.\)
C2H2 luôn pư với AgNO3/NH3.
Ta có: \(n_{Ag_2C_2}=n_{C_2H_2}=0,18\left(mol\right)\Rightarrow m_{Ag_2C_2}=0,18.240=43,2\left(g\right)=m_{\downarrow}\)
→ C4H6 không pư.
Vậy: CTCT đúng của 2 chất là: \(CH\equiv CH\) và \(CH_3-C\equiv C-CH_3\)

nCO2=8,96/22,4=0,4 mol
=> nC=nCO2=0,4 mol
mC=0,4.12=4,8g
=> mH=5,8-4,8=1g
nH=1 mol -> nH2O=0,5
nH=0,5 mol
Pt: CnH2n+2 + (3n+1/2)O2-> nCO2 + (n+1)H2O
0,4 0,5 mol
=> n/0,4=n+1/0,5 -> n=4
Vậy cthh cần tìm là C4H10

a) \(n_{O_2}=\dfrac{21,056}{22,4}=0,94\left(mol\right)\)
\(n_{CaCO_3}=\dfrac{52}{100}=0,52\left(mol\right)\)
BTNT C: \(n_C=n_{CO_2}=n_{CaCO_3}=0,52\left(mol\right)\)
BTNT O: \(n_{H_2O}=2n_{O_2}-2n_{CO_2}=0,84\left(mol\right)\)
\(\Rightarrow n_{ankan}=n_{H_2O}-n_{CO_2}=0,32\left(mol\right)\)
\(\Rightarrow\text{Số }\overline{C}_{\text{trung bình}}=\dfrac{n_C}{n_{ankan}}=\dfrac{0,52}{0,32}=1,625\)
Vì 2 ankan liên tiếp nhau trong dãy đồng đẳng nên 2 ankan là CH4 (metan) và C2H6 (etan)
b) BTNT H: \(n_H=2n_{H_2O}=1,68\left(mol\right)\)
Gọi \(\left\{{}\begin{matrix}n_{CH_4}=a\left(mol\right)\\n_{C_2H_6}=b\left(mol\right)\end{matrix}\right.\left(a,b>0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}n_C=n_{CH_4}+2n_{C_2H_6}=a+2b=0,52\\n_H=4n_{CH_4}+6n_{C_2H_6}=4a+6b=1,68\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0,12\\b=0,2\end{matrix}\right.\left(TM\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CH_4}=\dfrac{0,12.16}{0,12.16+0,2.30}.100\%=24,24\%\\\%m_{C_2H_6}=100\%-24,24\%=75,76\%\end{matrix}\right.\)
c)
\(CH_4+Cl_2\xrightarrow[]{askt}CH_3Cl\left(\text{metyl clorua}\right)+HCl\\ C_2H_6+Cl_2\xrightarrow[]{askt}C_2H_5Cl\left(\text{etyl clorua}\right)+HCl\)

sr làm tắt wa mog bạn hiểu:3
đặt cttb của 2 axit : \(C_{\overline{n}}H_{2\overline{n}+1}COOH\) ( n>0)
np1 = 2nh2 = 0,35 (mol)
nc(p2) = nCO2 = nkt = 0,9 (mol)
mbình tăng = mco2 + mH2O = 56,7 (g)
=> nh2o = 0,95 (mol)
=> nrượu = nh2o - nco2 = 0,05 (mol)
=>nhh axit = 0,35 - 0,05 = 0,3 (mol)
có : nc (axit) = tổng nc - nc(rượu) = 0,9 - 2.0,05 = 0,8 (mol)
=> \(\overline{n}+1=\dfrac{0,8}{0,3}=2,67\Rightarrow\overline{n}=1,67\)
vì 2 axit đồng đẳng kế tiếp => \(\left\{{}\begin{matrix}CH_3COOH\\C_2H_5COOH\end{matrix}\right.\)
đặt số mol 2 axit là x;y rồi giải hệ (hoặc làm đường chéo số c cũng đc)
=> từ đó tính %m

Đáp án A
Quy về đốt 0,22 mol đipeptit dạng CnH2nN2O3.
Bảo toàn O ||→ có (0,22 × 3 + 1,98 × 2) ÷ 3 = 1,54 mol CO2 = H2O ||→ nH2O trao đổi = 0,14 mol.
→ nE = 0,08 mol → E gồm 0,02 mol Xn và 0,06 mol Y10–n ||→ có 0,02n + 0,06(10 – n) = 0,44 → n = 4.
Lại để ý số Ctrung bình α-amino axit = 1,54 ÷ 0,22 ÷ 2 = 3,5 ||→ ∑nGly = ∑nVal.
Giả sử X4 là (Gly)a(Val)4–a và Y6 là (Gly)b(Val)6–b
→ có phương trình: a + 3b = (4 – a) + 3(6 – b) ||→ a + 3b = 11. Nghiệm nguyên duy nhất a = 2; b = 3.
Theo đó, trong Y có 3Gly và 3Val ||→ tỉ lệ là 1 : 1.

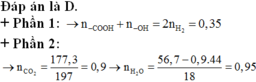
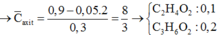
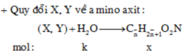
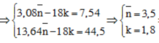
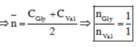
Bài 2 :
\(n_{CO2}=\frac{15,4}{44}=0,35\left(mol\right)\)
\(n_{H2O}=\frac{6,3}{18}=0,35\left(mol\right)\)
nCO2=nH2O
\(\rightarrow\) Hai hidrocacbon là anken
Gọi công thức chung là CnH2n 0,1mol
Ta có \(0,1n=n_{CO2}=0,35\left(mol\right)\)
\(\Rightarrow n=3,5\)
\(\rightarrow\) Hai anken là C3H6 và C4H8
C3H6 tác dụng với HBr cho hai sản phẩm
Mà khi cho tác dụng với HBr được ba sản phẩm
\(\rightarrow\) C4H8 tác dụng chỉ thu được 1 sản phẩm
\(\rightarrow\) C4H8 có cấu tạo đối xứng
\(\rightarrow\) CTCT là CH2=CH-CH3 và CH2-CH=CH-CH3