Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét `△BEM` và `△ CFM`:
\(\widehat{MEB}=\widehat{CFM}\)
`BM = MC`
\(\widehat{EBM}=\widehat{FCM}\)
`=>△BEM = △ CFM`
`=> BE = FC`
Ta có:
` AB = AE + EB`
` AC = AF + FC`
Mà `AB = AC` (vì △ABC cân tại A)
`EB = FC (cmt)`
`=> AE = AF`
`=>` △AEF` cân tại A
Xét `△AEM` và `△AFM` có:
AE = AF
\(\widehat{AEM}=\widehat{AFM}\)
AM cạnh chung
`=> △AEM =△AFM`
`=>` \(\widehat{EAM}=\widehat{FAM}\)
`=> AM là đường phân giác
Xét △AEF cân tại A có:
AM là đường phân giác
`=>` AM là trung trực của BC
b) Ta có: △AEM =△AFM
=> ME = MF
Xét △AEF cân tại A có:
AM là đường phân giác
=> AM là đường trung trực của EF

Bài làm :
a) Xét tam giác BEM và tam giác CFM
Ta có: BM = MC ( vì M là trung điểm của BC)
M là góc chung
Do đó : tam giác BEM=CFM( cạnh huyền- góc nhọn)
b) Bạn ghi chưa hết đề nên mik ko hiểu
sorry ![]()
![]()

Mình xin phép sửa đề:
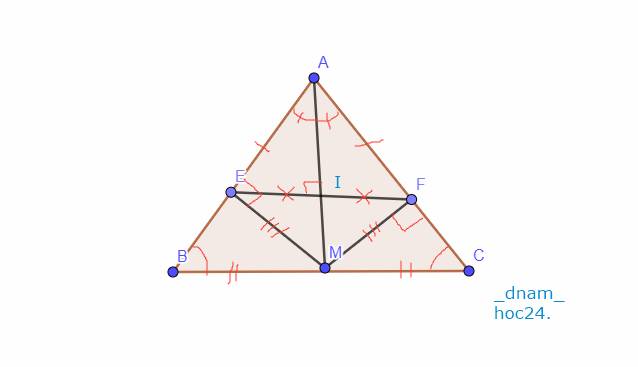
Cho tam giac ABC cân tại A, M là trung điểm của BC, ME vuông góc với AB, MF vuông góc với AC. Chứng minh ME = MF và AM là đường trung trực của EF.
\(\text {(1)}\)
Xét Tam giác `ABM` và Tam giác `ACM` có:
`AB = AC (\text {Tam giác ABC cân tại A})`
\(\widehat {B}= \widehat {C}(\text {Tam giác ABC cân tại A})\)
`MB = MC (\text {M là trung điểm của BC})`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`->`\(\widehat {BAM}=\widehat {CAM} (\text {2 góc tương ứng})\)
Xét Tam giác `AEM` và Tam giác `AFM` có:
`\text {AM chung}`
\(\widehat{BAM}=\widehat{CAM} (CMT)\)
\(\widehat{AEM}=\widehat{AFM} (=90^0)\)
`=> \text {Tam giác AEM = Tam giác AFM (ch-gn)}`
`-> ME = MF (2 cạnh tương ứng)`
\(\left(2\right)\)
Gọi `I` là giao điểm của `AM` và `EF`
C1:
Vì Tam giác `AEM =` Tam giác `AFM (\text {Theo CMT})`
`-> AE = AF (\text {2 cạnh tương ứng})`
Xét Tam giác `AEI` và Tam giác `AFI` có:
`AE = AF (CMT)`
\(\widehat{EAI}=\widehat{FAI} (\text {Theo CMT})\)
`\text {AI chung}`
`=> \text {Tam giác AEI = Tam giác AFI (c-g-c)}`
`-> IE = IF (\text {2 cạnh tương ứng})`
`->`\(\widehat{AIE}=\widehat{AIF} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{AIE}+\widehat{AIF}=180^0\)
`->`\(\widehat{AIE}=\widehat{AIF}=\)`180/2=90^0`
`-> \text {AI} \bot \text {EF}`
\(\text{Ta có: }\left\{{}\begin{matrix}\text{IE = IF }\\\text{AI}\perp\text{EF}\end{matrix}\right.\)
`-> \text {AI là đường trung trực của EF}`
`-> \text {AM là đường trung trực của EF}`
C2 (nếu bạn đã học về tính chất của tam giác cân với các đường Trung Tuyến, Đường Cao, Đường Trung Trực) :
Ta có:
AM vừa là đường phân giác, vừa là đường trung tuyến
`*` Theo tính chất của tam giác cân
`-> \text {AM là đường trung trực của EF (đpcm)}`
`@`\(\text{dnammv}\)

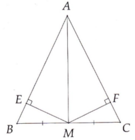
A B C E F M D
Vì tam giác ABC cân tại A
suy ra AB = AC, góc B = góc C
Xét tam giác vuông BME và tam giác vuông CMF
có Bm=CM (GT)
góc EBM = góc FCM ( CMT)
suy ta tam giác EBM = tam giác FCM ( cạnh huyền-góc nhọn)
suy ra EM=MF (hai cạnh tương ứng)
BE=CF (hai cạnh tương ứng)
mà BE+EA=AB, AF+FC=AC, lại có AB=AC
suy ra AE=AF
Xét tam giác AEM và tam giác AFM
có AE=AF (CMT)
AM chung
EM=FM ( CMT)
suy ra tam giác AEM = tam giác AFM (c.c.c) (*)
suy ra AE=AF suy ra A thuộc đường trung trực của EF (1)
mà MF=MF (CMT) suy ra M thuộc đường TT của EF (2)
Từ (1) và (2) suy ra AM là đường T.T của EF
b) Xét tam giác ABD và tam giác ACD
có AD chung
AB=AC (CMT)
góc ABD=góc ACD = 900
suy ra tam giác ABD và tam giác ACD (cạnh huyền-cạnh góc vuông)
suy ra góc BAD = góc CAD
suy ra AD là tia phân giác của góc BAC (3)
Từ (*) suy ra góc EAM = góc CAM
suy ra AM là tia phân giác của góc BAC (4)
Từ (3) và (4) suy ra AM trùng AD
suy ra A, M, D thẳng hàng

a) sửa đề => đường trung trực
ta có tg ABC cân tại A
M là trung điểm của BC
=> AM là đường trung trực của BC
=> AM là đường pg của tg ABC (t/c tg cân )
=> gBAM = gCAM hay gEAM = gFAM
xét tg AME và tg AMF có
gEAM = gFAM (cmt)
AM chung
gAEM = gAFM (=90o)
=> tg AME = tgAMF (cạnh huyền góc nhọn )
=> ME = MF (2 cạnh t/ư )
cho mình hỏi là: AM đâu phải là trung điểm đâu bạn có bị sai đề chỗ đấy không vậy