Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
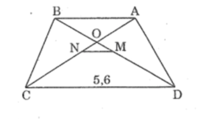
A B C D O M N 5,6
Xin lỗi Tú nhé hình mình vẽ chưa được cân lắm :( thông cảm
ABCD là hình thang cân nên AC = BD ; OA = OB ; OC = OD ; MN // AB // CD
\(MD=3.MO\Rightarrow OB=2.MO\) và \(OD=4.MO\)
Ta có : \(\frac{MN}{CD}=\frac{OM}{OD}=\frac{1}{4}\)\(\Rightarrow\)\(MN=\frac{1}{4}.CD=\frac{1}{4}.5,6=1,4\left(cm\right)\)
Mà \(\frac{AB}{CD}=\frac{OB}{OD}\Rightarrow\frac{AB}{CD}=\frac{1}{2}\)
\(\Rightarrow\)\(AB=\frac{1}{2}.CD=\frac{1}{2}.5,6=2,8\left(cm\right)\)
b) \(\frac{CD-AB}{2}=\frac{5,6-2,8}{2}=1,4\left(cm\right)\)
\(\Rightarrow\) \(MN=\frac{CD-AB}{2}\)
xong rùi nhé có gì sai sót bỏ qua dùm cái
Lời giải
a)
Ta có \(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\) \(\Rightarrow\)MN//DC
\(\Rightarrow\Delta OMN\approx\Delta ODC\approx OBA\)
Tỷ số đồng dạng
\(\dfrac{OM}{OD}=\dfrac{MN}{DC}=\dfrac{ON}{OC}\)\(\Rightarrow MN=\dfrac{OM}{OD}.DC=\dfrac{1}{4}.5,6=1,4\left(cm\right)\)
\(\dfrac{OM}{OB}=\dfrac{MN}{AB}\Rightarrow AB=\dfrac{OB}{OM}.MN=2MN=2,8\left(cm\right)\)
b)
\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\dfrac{CD-AB}{2}=\dfrac{4MN-2MN}{2}=MN\)
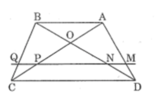
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: 
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: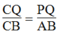 
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: 
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra 
hay MN = PQ.
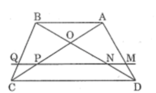
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: 
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: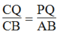 
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: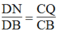 
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra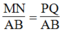 
hay MN = PQ.
a: DN/BD=DM/DA
CP/CA=CQ/CB
mà DM/DA=CQ/CB
nên DN/BD=CP/CA
b: Xét ΔDAB có MN//AB
nên MN/AB=DM/DA
Xet ΔCAB có PQ//AB
nên PQ/AB=CQ/CP
mà DM/DA=CQ/CP
nên MN=PQ
Xét Tam giác ADB: MN // AB (gt)
Suy ra: DN/DB = MN/AB (Hệ quả định lí Talét) (1)
Xét Tam giác ACB: PQ // AB (gt)
Suy ra: CQ/CB = PQ/AB (Hệ quá định lí Talét) (2)
Ta có: NQ sog sog AB (gt)
AB sog sog CD (gt)
Suy ra: NQ sog sog CD (cùng sog sog AB)
Xét Tam giác BDC: NQ sog sog CD (cmt)
Suy ra: DN/DB = CQ/CB (Định lí Talét) (3)
Từ (1), (2) và (3) suy ra: MN/AB = PQ/AB
Suy ra: MN = PQ (đpcm).