K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

22 tháng 4 2017
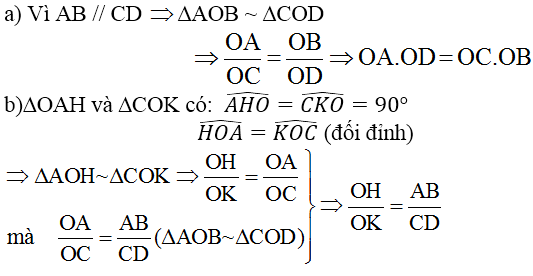
a;Vì AB//CD nên theo định lí Ta-lét ta có:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
\(\Rightarrow OA.OD=OC.OB\)
b;Xét \(\Delta AOH\) và \(\Delta COK\)có:
\(\widehat{AHO}=\widehat{CKO=90^o}\)
\(\widehat{AOH}=\widehat{COK}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta AOH~\Delta COK\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OH}{OK}\left(1\right)\)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\left(2\right)\)
Từ 1 và 2 ta có:
\(\dfrac{OH}{OK}=\dfrac{AB}{CD}\)
Bài 1:
a) Xét ΔOAB và ΔODC có
\(\widehat{OAB}=\widehat{ODC}\)(hai góc so le trong, AB//DC)
\(\widehat{AOB}=\widehat{DOC}\)(hai góc đối đỉnh)
Do đó: ΔOAB∼ΔODC(g-g)
⇒\(\frac{OA}{OD}=\frac{OB}{OC}\)
hay \(OA\cdot OC=OB\cdot OD\)(đpcm)
b) Xét ΔAHO và ΔDKO có
\(\widehat{AHO}=\widehat{DKO}\left(=90^0\right)\)
\(\widehat{AOH}=\widehat{DOK}\)(hai góc đối đỉnh)
Do đó: ΔAHO∼ΔDKO(g-g)
⇒\(\frac{OH}{OK}=\frac{AO}{DO}\)(các cặp cạnh tương ứng)
mà \(\frac{AO}{DO}=\frac{AB}{CD}\)(ΔOAB∼ΔODC)
nên \(\frac{OH}{OK}=\frac{AB}{CD}\)(đpcm)
Bài 2:
Bài 3:
a) Xét ΔAHB và ΔBCD có
\(\widehat{AHB}=\widehat{BCD}\left(=90^0\right)\)
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//DC)
Do đó: ΔAHB∼ΔBCD(g-g)
b) Xét ΔADH và ΔBDA có
\(\widehat{ADH}\) chung
\(\widehat{AHD}=\widehat{BAD}\left(=90^0\right)\)
Do đó: ΔADH∼ΔBDA(g-g)
⇒\(\frac{AD}{BD}=\frac{DH}{DA}\)
hay \(AD^2=BD\cdot DH\)(đpcm)
c) Áp dụng định lí pytago vào ΔADB vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow BD^2=6^2+8^2=100\)
\(\Leftrightarrow BD=\sqrt{100}=10cm\)
Ta có: \(AD^2=BD\cdot DH\)(cmt)
⇔\(6^2=10\cdot DH\)
hay \(DH=\frac{6^2}{10}=3,6cm\)
Áp dụng định lí pytago vào ΔAHD vuông tại H, ta được:
\(AD^2=AH^2+DH^2\)
\(\Leftrightarrow AH^2=AD^2-DH^2=6^2-3.6^2=23,04\)
hay \(AH=\sqrt{23,04}=4,8cm\)
Vậy: DH=3,6cm; AH=4,8cm