Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(\dfrac{-3}{5}\)
b. \(\dfrac{-2}{3}\) c. \(\dfrac{4}{39}\) d. \(\dfrac{26}{45}\)

a: \(\dfrac{5}{24}< \dfrac{15}{24}=\dfrac{5}{8}\)
b: \(\dfrac{6+9}{6\cdot9}=\dfrac{15}{54}\)
4/9=24/54
2/3=36/54
Do đó: \(\dfrac{15}{54}< \dfrac{24}{54}< \dfrac{36}{54}\)

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

d, Vì B=10^1993+1/10^1992+1 > 1 =>10^1993+1/10^1992+1>10^1993+1+9/10^1992+1+9 = 10^1993+10/10^1992+10= 10. (10^1992+1)/10. (10^1991+1) = 10^1992+1/10^1991+1=A Vậy A=B
cau d B>1 ta co tinh chat (\(\dfrac{a}{b}>\dfrac{a+m}{b+m}\) ) B> \(\dfrac{10^{1993}+1+9}{10^{1992}+1+9}\)\(=\dfrac{10^{1993}+10}{10^{1992}+10}\)=\(\dfrac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}\)=\(\dfrac{10^{1992}+1}{10^{1991}+1}\)=A
Suy ra B>A(chuc ban hoc goi nhe)

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)
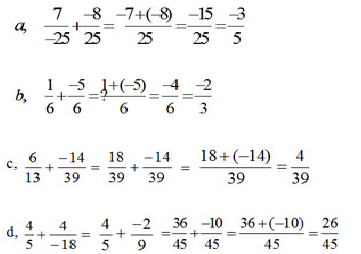
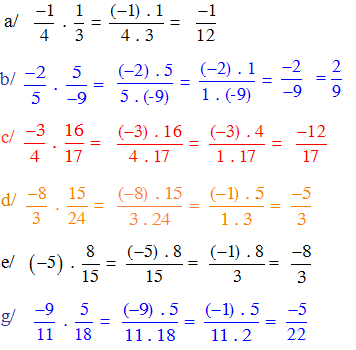
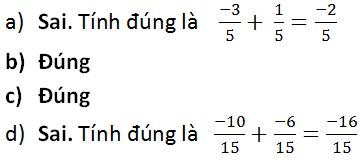
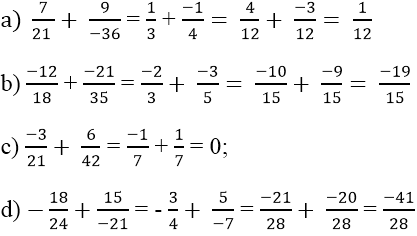


Bài 1:
a) \(a=2\cdot3\cdot5\cdot43\)
\(b=7200=2^5\cdot3^2\cdot5^2\)
\(c-4680=2^3\cdot3^2\cdot5\cdot13\)
b) \(\dfrac{8440}{5910}=\dfrac{8440:10}{5910:10}=\dfrac{844}{591}\)
\(\dfrac{1245}{3450}=\dfrac{1245:15}{3450:15}=\dfrac{83}{230}\)
Bài 2:
a) Ước nguyên tố của 140 là:
\(ƯNT\left(140\right)=\left\{2;5;7\right\}\)
Ước nguyên tố của 138 là:
\(ƯNT\left(138\right)=\left\{3;23;2\right\}\)
b) \(A=\dfrac{2^{10}+4^6}{8^4}\)
\(A=\dfrac{2^{10}+2^{12}}{2^{12}}\)
\(A=\dfrac{2^{10}\cdot\left(1+2^2\right)}{2^{12}}\)
\(A=\dfrac{1+4}{2^2}\)
\(A=\dfrac{5}{4}\)
\(B=\dfrac{6^{10}+15\cdot2^{10}\cdot3^9}{12\cdot8^3\cdot27^3}\)
\(B=\dfrac{2^{10}\cdot3^{10}+5\cdot2^{10}\cdot3^{10}}{2^{11}\cdot3^{10}}\)
\(B=\dfrac{2^{10}\cdot3^{10}\cdot\left(1+5\right)}{2^{11}\cdot3^{10}}\)
\(B=\dfrac{1+5}{2}\)
\(B=3\)