Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số thứ nhất bằng \(\dfrac{28}{33}:\dfrac{7}{9}=\dfrac{12}{11}\) số thứ hai.
Số 9 chính là giá trị của \(\dfrac{12}{11}-1=\dfrac{1}{11}\) số thứ hai.
Số thứ hai là: \(9:\dfrac{1}{11}=99\).
Số thứ nhất là: \(99+9=108\).

Gọi hai số cần tìm là a và b.
Suy ra : a = 258 – 126 = 132

Ta có:
\(a:\frac{6}{7}=a.\frac{7}{6}=\frac{7a}{6}\)là số tự nhiên => 7a chia hết cho 6
Mà (7;6)=1 => a chia hết cho 6 (1)
\(a:\frac{10}{11}=a.\frac{11}{10}=\frac{11a}{10}\)là số tự nhiên => 11a chia hết cho 10
Mà (11;10)=1 => a chia hết cho 10 (2)
Từ (1) và (2) => \(a\in BC\left(6;10\right)\)
Mà a nhỏ nhất => a = BCNN(6;10) = 30
Vậy a = 30
Vì a: \(\frac{6}{7}\)= Z => \(a.\frac{7}{6}\)= Z=> a thuộc B (6)
vì \(a:\frac{10}{11}=Z=>a.\frac{11}{10}=Z\)=>chữ số hàng đơn vị của a là 0
Để thỏa mãn thì a = 30 vì \(30\in B\left(6\right)\)là STN nhỏ nhất có chữ số 0 bên hàng đơn vị

\(a:\frac{6}{7}\)\(=\frac{7a}{6}\) Mà ƯCLN(7;6)=1 nên \(a\in\) B(6)
\(a:\frac{10}{11}=\frac{11a}{10}\) Mà ƯCLN(10;11)=1 nên a\(\in\) B(10)
Để A nhỏ nhất \(\Leftrightarrow\) A=BCNN(6;10)=30
Vậy số A phải tìm là 30
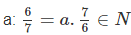 nên 7a ⋮ 6 suy ra a ⋮ 6 (vì 7 và 6 là nguyên tố cùng nhau);
nên 7a ⋮ 6 suy ra a ⋮ 6 (vì 7 và 6 là nguyên tố cùng nhau);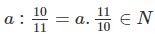 nên 11a ⋮ 10 suy ra a ⋮ 10 (vì 11 và 10 nguyên tố cùng nhau). Như vậy a là bội chung của 6 và 10.
nên 11a ⋮ 10 suy ra a ⋮ 10 (vì 11 và 10 nguyên tố cùng nhau). Như vậy a là bội chung của 6 và 10.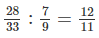 số thứ hai.
số thứ hai.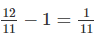 số thứ hai.
số thứ hai.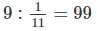
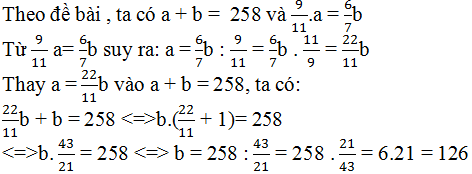
Bài 2:
Tỉ số của số thứ nhất và số thứ hai là:
28/33:7/9=12/11
Số thứ nhất là 9:1x12=108
Số thứ hai là 108-9=99