Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A và B là hai điểm dân cư, C là điểm đặt trạm y tế.

Vì C cách đều AB nên C thuộc đường trung trực của AB mà C ∈ xy nên C là giao điểm của xy và đường trung trực của AB
gọi 2 điểm dân cư đó là A và B, trạm y tế là C.
để C cách đểu A và B thì C phải thuộc đường trung trực của AB.
khi đó để được điểm C nằm trên đường quốc lộ và cách đều 2 điểm A,B thì C phải trùng với giao điểm của đường trung trực của AB và đường quốc lộ.
vậy trạm y tế được đặt ở giao điểm của đường quốc lộ và đường trung trực của AB.

Ba góc tại mỗi đỉnh chung của ba tam giác tạo thành góc bẹt
Do đó, tổng của chúng bằng 180 độ.
Ta thấy ba điểm A, B, C thẳng hàng.

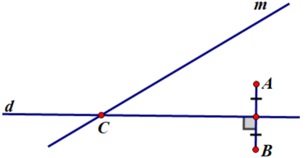
Gọi A và B là hai điểm dân cư ; C là điểm đặt trạm y tế ; m là đường quốc lộ
Vì C cách đều AB nên C thuộc đường trung trực của AB
mà C ∈ d nên C là giao điểm của d và đường trung trực (d) của AB.
Gọi 2 điểm dân cư là hai điểm A, B. Để xây dựng trạm y tế ở bên đường cách đều hai điểm dân cư thì trạm y tế đó phải là giao điểm giữa con đường và đường trung trực của AB.

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

Ta có: \(\frac{{33}}{{12}} = \frac{{165}}{{60}};\frac{{79}}{{30}} = \frac{{158}}{{60}}\)
Vì 158 < 165 nên \(\frac{{158}}{{60}} < \frac{{165}}{{60}}\) hay 0 < \(\frac{{79}}{{30}} < \frac{{33}}{{12}}\)
Vì \( - \frac{{25}}{{12}} < - 1\) và \( - 1 < - \frac{5}{6}\) nên \( - \frac{{25}}{{12}} < - \frac{5}{6} < 0\)
Như vậy, độ cao của:
Điểm D: \( - \frac{{25}}{{12}}\) (km)
Điểm E: \( - \frac{5}{6}\) (km)
Điểm C: 0 (km)
Điểm A: \(\frac{{79}}{{30}}\) (km)
Điểm B: \(\frac{{33}}{{12}}\) (km)

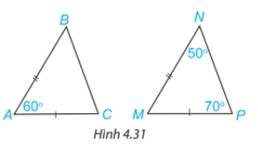
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
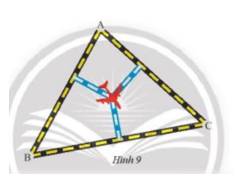



Theo đề bài ta có 3 thành phố tạo thành 1 hình tam giác và các cạnh của tam giác đó là các xa lộ
Người ta muốn xây sân bay cách đều 3 xa lộ nên điểm đó sẽ cách đều 3 cạnh của tam giác
\( \Rightarrow \) Điểm đó là giao điểm của 3 phân giác trong tam giác ABC
Để xác định được điểm đặt saan bay ta phải vẽ các tia phân giác từ các đỉnh của tam giác ABC chúng cắt nhau ở đâu thì đó chính là điểm cần xây sân bay thỏa mãn yêu cầu