Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi tiền lãi của mỗi đơn vị là a, b, c (triệu đồng) và a, b, c > 0
Vì tiền lãi được chia tỉ lệ với vốn đầu tư nên a, b, c tỉ lệ với 2, 5 và 7 do đó 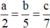
Số tiền lãi là 560 triệu, nghĩa là a + b + c = 560.
Theo tính chất của dãy tỉ số bằng nhau ta có :
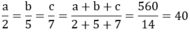
Suy ra:
a = 2.40 = 80
b = 5.40 = 200
c = 7.40 = 280
Vậy tiền lãi của mỗi đơn vị lần lượt là 80 triệu, 200 triệu, 280 triệu.

Gọi a, b, c là tiền lãi của mỗi đơn vị.
Vì tiền lãi được chia tỉ lệ với vốn đầu tư nên a, b, c tỉ lệ với 2, 5 và 7 do đó:
a2=b5=c7a2=b5=c7 và a +b +c = 560
⇒a2=b5=c7=a+b+c2+5+7=56014=40⇒a2=b5=c7=a+b+c2+5+7=56014=40
Suy ra: a = 2.40 = 80
b = 5.40 =200
c = 7.40 = 280
Vậy số tiền lãi của mỗi đơn vị lần lượt là 80 triệu, 200 triệu, 280 triệu.
Em cảm ơn ạ!!!~
Gọi a, b, c là tiền lãi của mỗi đơn vị.
Vì tiền lãi được chia tỉ lệ với vốn đầu tư nên a, b, c tỉ lệ với 2, 5 và 7 do đó:
a2=b5=c7a2=b5=c7 và a +b +c = 560
⇒a2=b5=c7=a+b+c2+5+7=56014=40⇒a2=b5=c7=a+b+c2+5+7=56014=40
Suy ra: a = 2.40 = 80
b = 5.40 =200
c = 7.40 = 280
Vậy số tiền lãi của mỗi đơn vị lần lượt là 80 triệu, 200 triệu, 280 triệu.

Gọi a, b, c là tiền lãi của mỗi đơn vị.
Vì tiền lãi được chia tỉ lệ với vốn đầu tư nên a, b, c tỉ lệ với 2, 5 và 7 do đó:
\(\frac{a}{2}\)=\(\frac{b}{5}\)=\(\frac{c}{7}\) và a +b +c = 560
⇒\(\frac{a}{2}\)=\(\frac{b}{5}\)=\(\frac{c}{7}\)=\(\frac{a+b+c}{2+5+7}\)=\(\frac{560}{14}\)=40
Suy ra: a = 2.40 = 80
b = 5.40 =200
c = 7.40 = 280
Vậy số tiền lãi của mỗi đơn vị lần lượt là 80 triệu, 200 triệu, 280 triệu.
Gọi a, b, c là tiền lãi của mỗi đơn vị.
Vì tiền lãi được chia tỉ lệ với vốn đầu tư nên a, b, c tỉ lệ với 2, 5 và 7 do đó:
a2=b5=c7a2=b5=c7 và a +b +c = 560
⇒a2=b5=c7=a+b+c2+5+7=56014=40⇒a2=b5=c7=a+b+c2+5+7=56014=40
Suy ra: a = 2.40 = 80
b = 5.40 =200
c = 7.40 = 280
Vậy số tiền lãi của mỗi đơn vị lần lượt là 80 triệu, 200 triệu, 280 triệu.

Gọi số lãi của ba đơn vị được chia lần lượt là a,b,c (triệu đồng )
a = 2.40 = 80
b = 5.40 = 200
c = 7.40 = 280
Vậy đơn vị 1, đơn vị 2, đơn vị 3 có số tiền lãi lần lượt là :
80; 200; 280 (triệu đồng)
Gọi số lãi của ba đơn vị được chia lần lượt là a,b,c (triệu đồng )
a = 2.40 = 80
b = 5.40 = 200
c = 7.40 = 280
Vậy đơn vị 1, đơn vị 2, đơn vị 3 có số tiền lãi lần lượt là :
80; 200; 280 (triệu đồng)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{2+5+7}=\dfrac{560000000}{14}=40000000\)
Do đó: a=80000000; b=200000000; c=280000000

Gọi a,b,c (triệu đồng) lần lượt là số tiền lãi của 3 đơn vị (0 < a, b, c < 450).
Tổng số tiền lãi là 450 triệu đồng nên a+b+c = 450
Vì số tiền lãi tỉ lệ thuận với số vốn đã góp nên ta có:
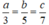
Theo tính chất của dãy tỉ số bằng nhau ta có:
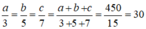
a/3 = 30 ⇒ a = 3.30 = 90
b/5 = 30 ⇒ b = 5.30 = 150
c/7 = 30 ⇒ c = 7.30 = 210
Vậy số tiền lãi được chia cho các đơn vị theo thứ tự là 90 triệu; 150 triệu và 210 triệu

Gọi số tiền vốn lần lượt là a,b,c(đồng)
Đk:a,b,c<450
a,b,c thuộc N*
Theo bài ra, ta có:
a/3=b/5=c/7 và a+b+c=450
Theo tính chất dãy tỉ số bằng nhau, ta có:
a/3=b/5=c/7=a+b+c/3+5+7=450/15=30
Với:
a/3=30=>a=3.30=90
b/5=30=>b=5.30=150
c/7=30=>c=7.30=210

gọi 3 đơn vị kinh doanh là x y z
x/3 = y/5 = z/7 x+y+z=450 tr
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/3 = y/5 = z/7 ; x/3+y/5+z/7 = 450/15 =30
x=30*3=60
y=30*5=150
z=30*7=350
vậy 3 đơn vị kinh doanh góp số vốn lần lượt là 60;150;350
like cho mik nha!

Gọi số tiền lãi mà ba đơn vị được chia là x, y, z
Theo đề bài ta có:
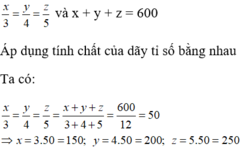
Chọn đáp án D
Vốn đầu tư của 3 đơn vị theo tỉ lệ 2: 3 : 7
Tiền lãi được chia tỉ lệ thuận với vốn đầu tư nên
tiền lãi thu được của 3 đơn vị theo thứ tự trên cũng theo tỉ lệ 2 : 3: 7
Gọi x; y ; z là tiền lãi của đơn vị 1; 2; 3
=> x : y : z = 2 : 3: 7 hay \(\frac{x}{2}=\frac{y}{3}=\frac{z}{7}\)
Theo đề bài: x + y + z = 560
Áp dụng dãy tỉ số bằng nhau => \(\frac{x}{2}=\frac{y}{3}=\frac{z}{7}=\frac{x+y+z}{2+3+7}=\frac{560}{12}=\frac{140}{3}\)
=> \(\frac{x}{2}=\frac{140}{3}\Rightarrow x=\frac{280}{3}\) triệu
\(\frac{y}{3}=\frac{140}{3}\Rightarrow y=140\) triệu
\(\frac{z}{7}=\frac{140}{3}\Rightarrow z=\frac{980}{3}\) triệu
Vậy ....................