
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
∆AHB và ∆KBH có
AH=KH ( gt )
=
BH cạnh chung .
Nên ∆AHB=∆KBH(c.g.c)
Suy ra: =
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC ( c . g . c )
Suy ra: =
Vậy CH là tia phân giác của góc C
p/s: Very làm biếng open sách so copy mạng =]]]

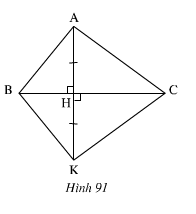
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=>
hay DK là phân giác
=> =
∆ADI = ∆BDI (c.c.c)
=>
=> DI là phân giác
=> =
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay + = 900
Do đó + = 900
=> + = 1800
Xem thêm tại: http://loigiaihay.com/bai-55-trang-80-sgk-toan-lop-7-tap-2-c42a5841.html#ixzz44NZ9vg5o


bạn cứ gõ lên goole bài 45 sgk tr99 toán 7 tập 1 sẽ có . tick nha

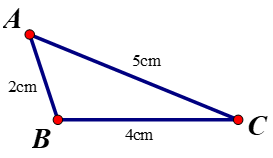
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
2)heo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Kiến thức áp dụng
+ Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Định lý tổng ba góc trong tam giác: Trong một tam giác, tổng ba góc bằng 180º.
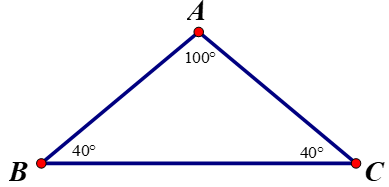
3 a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
b) Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có
4) Trong một tam giác ta luôn có:
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn
⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.
+ Góc nhỏ nhất luôn là góc nhọn.
(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn
⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.
5) + Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.
6)Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
7)
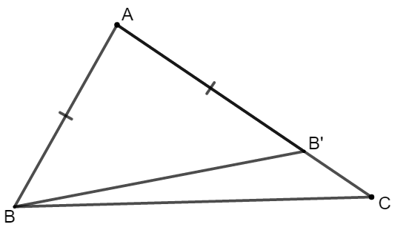
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.
c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C


TL
a) Ta có ˆBIKBIK^ là góc ngoài tại đỉnh II của ΔBAIΔBAI.
Nên ˆBIK=ˆBAI+ˆABI>ˆBAIBIK^=BAI^+ABI^>BAI^
Mà ˆBAK=ˆBAIBAK^=BAI^
Vậy ˆBIK>ˆBAKBIK^>BAK^ (1)
b) Ta có ˆCIKCIK^ là góc ngoài tại đỉnh II của ΔAICΔAIC
nên ˆCIK=ˆCAI+ˆICA>ˆCAICIK^=CAI^+ICA^>CAI^
Hay ˆCIK>ˆCAICIK^>CAI^ (2)
Từ (1) và (2) ta có:
ˆBIK+ˆCIK>ˆBAK+ˆCAIBIK^+CIK^>BAK^+CAI^
⇒ˆBIC>ˆBAC⇒BIC^>BAC^.
Hok tốt nha bn
#Kirito

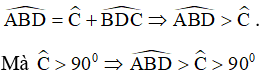
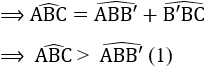
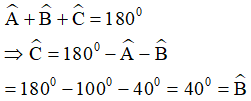

A B D E C x y
\(Xét\Delta ABCvà\Delta ADEcó:\)
AB=AD
góc A chung
AC=AE
\(\Rightarrow\Delta ABC=\Delta ADE\) (c-g-c)