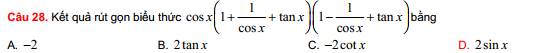Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vì \(90^o< x< 180^o\Rightarrow\cos x< 0\)
Có: \(\sin^2x+\cos^2x=1\Leftrightarrow\left(\dfrac{2}{5}\right)^2+\cos^2x=1\Leftrightarrow\cos^2x=\dfrac{21}{25}\Leftrightarrow\cos x=-\dfrac{\sqrt{21}}{5}\left(vì\cos x< 0\right)\)


1:
-x^2+x+6<=0
=>x^2-x-6>=0
=>(x-3)(x+2)>=0
=>x>=3 hoặc x<=-2
2:
Phương trình tổng quát của (d) là:
x=1+t và y=-3+4t


cosx(1 + 1/cosx + tanx)(1 - 1/cosx + tanx)
= cosx[(1 + tanx)² - 1/cos²x]
= cosx(1 + tan²x + 2tanx - 1 - tan²x)
= 2tanxcosx
= 2sinxcosx/cosx
= 2sinx
Chọn D
\(=cosx\left(1+\dfrac{1}{cosx}+\dfrac{sinx}{cosx}\right)\left(1-\dfrac{1}{cosx}+\dfrac{sinx}{cosx}\right)\)
\(=cosx\left(\dfrac{sinx+1+cosx}{cosx}\right)\left(\dfrac{cosx+sinx-1}{cosx}\right)\)
\(=\left(cosx+sinx\right)^2\)\(-1\)
\(=cos^2x+2cosxsinx+sin^2x-1\)
\(=cos^2x+sin^2x+2cosxsinx-1\)
\(=1+2cosxsinx-1\)
\(=2cosxsinx\)
Áp dụng đẳng thức góc nhân đôi cho sin
\(=2sinx\)

Hiểu như này:
\(\dfrac{a}{1+a}+\dfrac{b}{1+b}+\dfrac{b}{1+b}=3-\left(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+b}\right)\le3-\dfrac{9}{1+a+1+b+1+b}=\dfrac{3\left(a+2b\right)}{3+a+2b}\)