Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| GT | \(\widehat{xOy}=180^0\) Om,On lần lượt là p/g \(\widehat{xOz};\widehat{yOz}\) |
| KL | \(Om\perp On\) |

1,Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
⇒{ˆO1=ˆO2=12.ˆxOyˆO3=ˆO4=12.ˆyOz⇒{O1^=O2^=12.xOy^O3^=O4^=12.yOz^
⇒ˆO2+ˆO3=12(ˆxOy+ˆyOz)=12.1800=900⇒O2^+O3^=12(xOy^+yOz^)=12.1800=900
=> Đpcm

Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
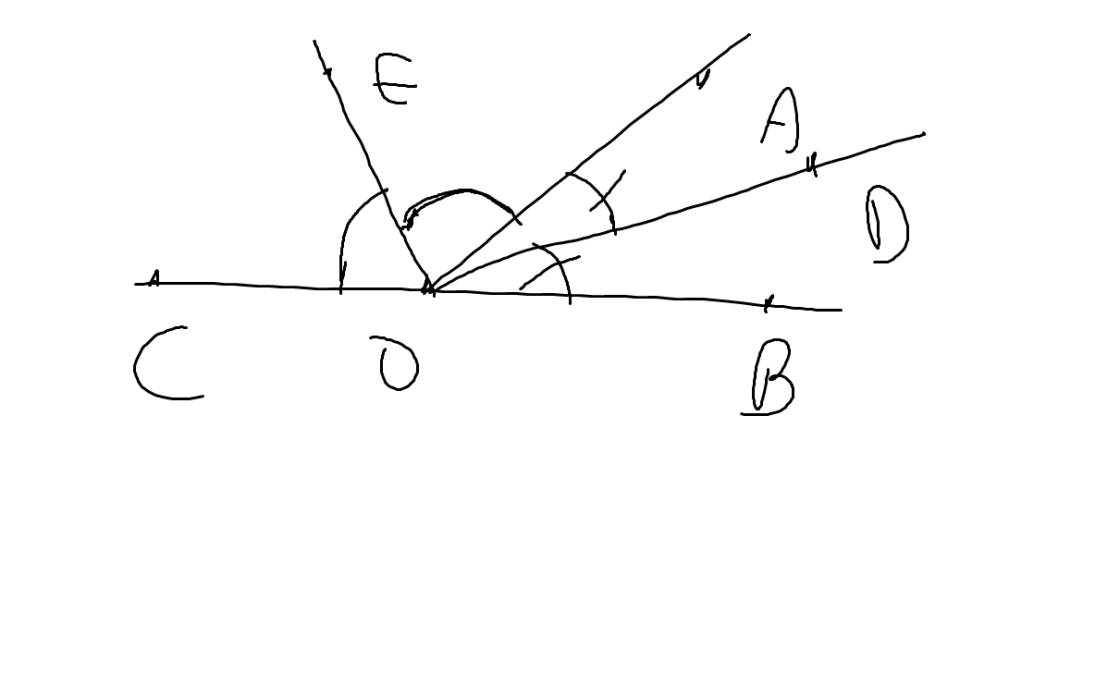
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)

Gọi : góc xOy kề bù với góc yOz . Ot là tia phân giác của góc xOy . Ot' là tia phân giác của góc xOz (bạn tự vẽ hình nha).
Ta có :
Do Ot là tia phân giác của góc xOy nên góc \(xOt=tOy=\frac{1}{2}xOy\) .
Do Ot' là tia phân giác của góc yOz nên góc \(yOt'=t'Oz=\frac{1}{2}yOz\).
\(\Leftrightarrow\) Góc \(tOy+yOt'=\frac{1}{2}xOy+\frac{1}{2}yOz=\frac{1}{2}\left(xOy+yOz\right)\) .
Mà \(xOy+yOz=180\left(độ\right)\) .
Do đó : \(tOy+yOt'=\frac{1}{2}\left(xOy+yOz\right)=\frac{1}{2}.180\left(độ\right)=90\left(độ\right)\) .
Vậy : Hai tia phân giác của 2 góc kề bù vuông góc với nhau .
Gọi \(\widehat{xOy}\) và \(\widehat{yOz}\) là hai góc kề bù, Om và On lần lượt là hai tia phân giác của hai góc đó
Vì Om và On lần lượt là các tia phân giác của \(\widehat{xOy}\) và nên
\(\begin{cases}\widehat{mOy}=\frac{1}{2}\widehat{xOy}\\\widehat{yOn}=\frac{1}{2}\widehat{yOz}\end{cases}\) => \(\begin{cases}2\widehat{mOy}=\widehat{xOy}\\2\widehat{yOn}=\widehat{yOz}\end{cases}\)
Ta lại có \(\widehat{xOy}+\widehat{yOz}\) = 180 độ (vì \(\widehat{xOy}\) và \(\widehat{yOz}\) là hai góc kề bù)
=> 2\(\widehat{mOy}\) +2\(\widehat{yOn}\) =180
=>2(\(\widehat{mOy}+\widehat{yOn}\))=180
=>\(\widehat{mOy}+\widehat{yOn}\) = 90
=>Om vuông góc với On
=>đpcm

O x z y u v
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

x y z O m n
Cho \(\widehat{xOy};\widehat{yOz}\) là 2 góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{yOz}=180^0\)
Gọi Om ; On lần lượt là tia phân giác của 2 goc đó
\(\Rightarrow\begin{cases}\widehat{mOy}=\frac{1}{2}.\widehat{xOy}\\\widehat{nOy}=\frac{1}{2}.\widehat{yOz}\end{cases}\)
\(\Rightarrow\widehat{mOy}+\widehat{nOy}=\frac{\widehat{xOy}+\widehat{yOx}}{2}\)
\(\Rightarrow\widehat{mOn}=\frac{180^0}{2}\)
\(\Rightarrow\widehat{mOn}=90^0\)
=> đpcm
Ta có :
Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
=> Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau

O A B C M N
Gọi AOC và COB là hai góc kề bù , OM và ON theo thứ tự là các tia phân giác của hai góc ấy . Ta có :
\(\widehat{MOC}+\widehat{CON}=\frac{\widehat{AOC}}{2}+\frac{\widehat{COB}}{2}=\frac{\widehat{AOC}+\widehat{COB}}{2}=\frac{180^0}{2}=90^0\)
Ta thấy tia OC nằm giữa hai tia OM và ON nên \(\widehat{MOC}+\widehat{CON}=\widehat{MON}\)
Do đó MON = 900 . Vậy \(OM\perp ON\)
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
