Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Từ kết quả câu a, b ta được bảng sau:
Nhận xét:
- Các hàm số y = f(x) = 2/3 x và y = g(x) = 2/3 x + 3 là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
a) Cho hàm số : \(y=f\left(x\right)=\dfrac{2}{3}x\)
Ta có : \(f\left(-2\right)=\dfrac{2}{3}.\left(-2\right)=-\dfrac{4}{3}\)
\(f\left(-1\right)=\dfrac{2}{3}.\left(-1\right)=-\dfrac{2}{3}\)
\(f\left(0\right)=\dfrac{2}{3}.0=0\)
\(f\left(\dfrac{1}{2}\right)=\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\)
\(f\left(1\right)=\dfrac{2}{3}.1=\dfrac{2}{3}\)
\(f\left(2\right)=\dfrac{2}{3}.2=\dfrac{4}{3}\)
\(f\left(3\right)=\dfrac{2}{3}.3=2\)
b) Cho hàm số : \(y=g\left(x\right)=\dfrac{2}{3}x+3\)
\(g\left(-2\right)=\dfrac{2}{3}.\left(-2\right)+3=\dfrac{5}{3}\)
\(g\left(-1\right)=\dfrac{2}{3}.\left(-1\right)+3=\dfrac{7}{3}\)
\(g\left(0\right)=\dfrac{2}{3}.0+3=3\)
\(g\left(\dfrac{1}{2}\right)=\dfrac{2}{3}.\dfrac{1}{2}+3=\dfrac{10}{3}\)
\(g\left(1\right)=\dfrac{2}{3}.1+3=\dfrac{11}{3}\)
\(g\left(2\right)=\dfrac{2}{3}.2+3=\dfrac{13}{3}\)
\(g\left(3\right)=\dfrac{2}{3}.3+3=5\)
c) Khi \(x\)lấy cùng một giá trị thì giá trị của \(g\left(x\right)\) lớn hơn giá trị của \(f\left(x\right)\) là \(3\) đơn vị.

em xin lỗi nhưng em chưa đủ tuổi để làm bài này xin cáo từ
xin lỗi quản lý olm ạ
a) Ta có:
f(−2)=23.(−2)=−43;f(−1)=23.(−1)=−23;f(0)=23.0=0;f(12)=23.12=13;f(1)=23.1=23;f(2)=23.2=43;f(3)=23.3=2.f(−2)=23.(−2)=−43;f(−1)=23.(−1)=−23;f(0)=23.0=0;f(12)=23.12=13;f(1)=23.1=23;f(2)=23.2=43;f(3)=23.3=2.
b) Ta có:
g(−2)=23.(−2)+3=53;g(−1)=23.(−1)+3=73;g(0)=23.0+3=3;g(12)=23.12+3=103;g(1)=23.1+3=113;g(2)=23.2+3=133;g(3)=23.3+3=5.g(−2)=23.(−2)+3=53;g(−1)=23.(−1)+3=73;g(0)=23.0+3=3;g(12)=23.12+3=103;g(1)=23.1+3=113;g(2)=23.2+3=133;g(3)=23.3+3=5.
c) Khi biến xx lấy cùng một giá trị thì giá trị của hàm số y=f(x)y=f(x) luôn nhỏ hơn giá trị tương ứng của hàm số y=g(x)y=g(x) là 3 đơn vị.

a) Ta có:
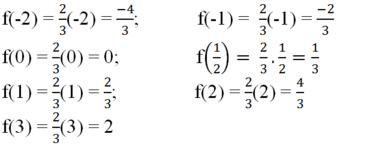
b) Ta có:
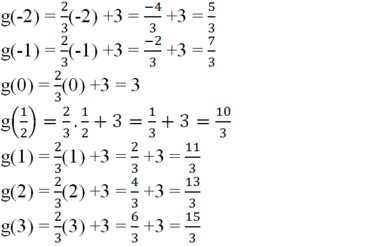
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
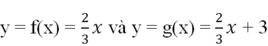
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.

a: f(1)=-1,5
f(2)=-6
f(3)=-13,5
=>f(1)>f(2)>f(3)
b: \(f\left(-3\right)=-1,5\cdot9=-13,5\)
f(-2)=-1,5x4=-6
f(-1)=-1,5x1=-1,5
=>f(-3)<f(-2)<f(-1)
c: Hàm số này đồng biến khi x<0 và nghịch biến khi x>0

Lời giải:
a)
\(f(-3)=(-3)^2=9; f(-\frac{1}{2})=(\frac{-1}{2})^2=\frac{1}{4}\)
\(f(0)=0^2=0\)
\(g(1)=3-1=2; g(2)=3-2=1; g(3)=3-3=0\)
b)
\(2f(a)=g(a)\)
\(\Leftrightarrow 2a^2=3-a\)
\(\Leftrightarrow 2a^2+a-3=0\Leftrightarrow (2a+3)(a-1)=0\)
\(\Rightarrow \left[\begin{matrix} a=\frac{-3}{2}\\ a=1\end{matrix}\right.\)

điều kiện xác định : \(x\ge0;x\ne1\)
a) ta có : \(G=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{x^2-2x+1}{2}\)
\(\Leftrightarrow G=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right).\dfrac{\left(x-1\right)^2}{2}\)
\(\Leftrightarrow G=\left(\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right).\dfrac{\left(x-1\right)^2}{2}\) \(\Leftrightarrow G=\left(\dfrac{-2\sqrt{x}}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right).\dfrac{\left(x-1\right)^2}{2}=\sqrt{x}-x\)
b) thay \(x=0,16\) vào \(G\) ta có : \(G=\sqrt{0,16}-0,16=0,24\)
c) ta có : \(G=-\left(x-\sqrt{x}+\dfrac{1}{4}\right)-\dfrac{1}{4}=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge\dfrac{-1}{4}\)
\(\Rightarrow G_{max}=\dfrac{-1}{4}\) khi \(\sqrt{x}=\dfrac{1}{2}\Leftrightarrow x=\dfrac{1}{4}\)
d) ta có : \(G=\sqrt{x}-x\) \(\Rightarrow\) để \(G\in Z\) \(\Rightarrow x=a^2\ne1\)
e) ta có : \(G>0\Leftrightarrow\sqrt{x}-x>0\Leftrightarrow\sqrt{x}\left(1-\sqrt{x}\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}>0\\1-\sqrt{x}>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}< 0\\1-\sqrt{x}< 0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}0< x< 1\\x\in\varnothing\end{matrix}\right.\) \(\Rightarrow\left(đpcm\right)\)
f) để \(G< 0\Leftrightarrow\sqrt{x}-x< 0\Leftrightarrow\sqrt{x}\left(1-\sqrt{x}\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}>0\\1-\sqrt{x}< 0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}< 0\\1-\sqrt{x}>0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x>1\\x\in\varnothing\end{matrix}\right.\) vậy \(x>1\)
bạn có thể làm chi tiết dòng thứ tư phần rút gọn đc ko ?

a, P=\(\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{\left(1-x\right)^2}{2}\)
\(P=\left(\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right).\dfrac{\left(1-x\right)^2}{2}\)
\(P=\dfrac{x-\sqrt{x}-2-\left(x+\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}.\dfrac{\left(1-x\right)^2}{2}\)
\(P=\dfrac{-2\sqrt{x}}{\left(x-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(x-1\right)^2}{2}\)
\(P=\dfrac{-\sqrt{x}\left(x-1\right)}{\sqrt{x}+1}=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}=-\sqrt{x}\left(\sqrt{x}-1\right)=\sqrt{x}-x\)b,x=\(7-4\sqrt{3}=4-2.2\sqrt{3}+3=\left(2-\sqrt{3}\right)^2\)
Thay vào ta có \(P=\sqrt{\left(4-\sqrt{3}\right)^2}-\left(7-4\sqrt{3}\right)\)
\(P=\left|4-\sqrt{3}\right|-7-4\sqrt{3}=4-\sqrt{3}-7+4\sqrt{3}\)
\(P=-3+3\sqrt{3}\)
Câu 2:
a: f(1)=2
=>m-1+2m-3=2
=>3m=6
=>m=2
=>f(x)=x+1
=>f(2)=2+1=3
b: f(-3)=0
=>-3m+3+2m-3=0
=>m=0
=>f(x)=-x-3
=>f(x) nghịch biến

Ta có \(f\left(1\right)+f\left(10\right)+f\left(100\right)=1+a+b+100+10a+b+10000+100a+b\)
\(=10101+111a+3b\)
Tương tự \(G\left(1\right)+G\left(10\right)+G\left(100\right)=10101+111m+3n\)
Từ đây ta có \(111a-3b=111m-3n\Rightarrow111\left(a-m\right)-3\left(b-n\right)=0\)
Xét \(h\left(x\right)=f\left(x\right)-G\left(x\right)\) , khi đó \(h\left(x_0\right)=f\left(x_0\right)-G\left(x_0\right)\)
\(=ax_0+b-mx_0-n=\left(a-m\right)x_0+\left(b-n\right)\)
Để \(h\left(x_0\right)=0\Rightarrow\left(a-m\right)x_0+\left(b-n\right)=0\Rightarrow3\left(a-m\right)x_0+3\left(b-n\right)=0\)
Ta đã có \(111a-3b=111m-3n\Rightarrow111\left(a-m\right)-3\left(b-n\right)=0\)
Vậy nên \(3x_0=111\Rightarrow x_0=37\)
Tóm lại \(f\left(37\right)=G\left(37\right)\)
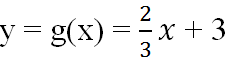
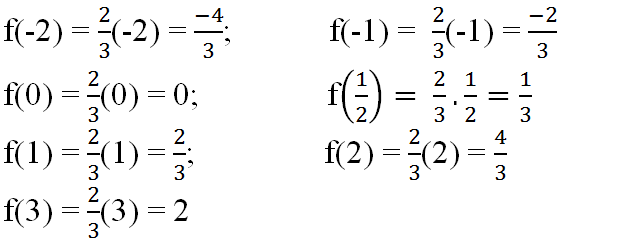
c: Ở hai hàm số trên, nếu lấy biến x cùng một giá trị thì f(x) sẽ nhỏ hơn g(x) 3 đơn vị