Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điện trở của đèn 1 và đèn 2 cùng loại là:
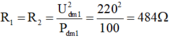
Điện trở tương đương của 2 đèn khi ghép nối tiếp là:
R 12 = R 1 + R 2 = 484 + 484 = 968Ω
Công suất của đoạn mạch nối tiếp là:
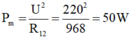
Do hai đèn giống nhau mắc nối tiếp nên công suất của mỗi bóng đèn là:
P 1 = P 2 = P m / 2 = 50/2 = 25 W

\(U_{mach}=U_{den}=220V\Rightarrow P_{den}=P_{dinhmuc}=60\)W
Chọn C

Điện trở của dây tóc bóng đèn Đ1 và Đ2:
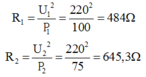
Điện trở tương đương của đoạn mạch mắc nối tiếp:
R = R1 + R2 = 484 + 645,3 = 1129,3 Ω
Cường độ dòng điện qua mạch:
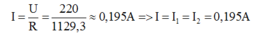
Hiệu điện thế giữa hai đầu đèn Đ1 và Đ2:
U1 = I.R1 = 0,195.484 = 94,38V
U2 = I.R2 = 0,195.645,3 = 125,83V
Công suất của đoạn mạch:
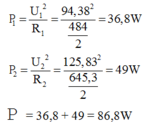
→ Đáp án A

Đ 1 mắc /nt Đ 2 , khi đó điện trở của mỗi đèn là:
R ' 1 = 50% R 1 = 0,5.484 = 242Ω; R ' 2 = 50% R 2 = 0,5.645,33 = 322,67Ω
Điện trở tương đương của đoạn mạch nối tiếp:
R ' = R ' 1 + R ' 2 = 242 + 322,67 = 564,67Ω
Cường độ dòng điện qua mạch: I ' = U / R ' = 220 / 564,67 ≈ 0,39A
⇒ I ' = I ' 1 = I ' 2 = 0,39A.
Hiệu điện thế giữa hai đầu đèn Đ 1 và Đ 2 :
U ' 1 = I ' . R ' 1 = 0,39.242 = 94,38V.
U ' 2 = I ' . R ' 2 = 0,39.322,67 = 125,84V.
Công suất điện của đoạn mạch: P n t = U ' . I ' = 220.0,39 = 85,8W

\(R_{Đ1}=\dfrac{U^2_{Đ1}}{P_{Đ1}}=\dfrac{220^2}{100}=484\Omega\)
\(R_{Đ2}=\dfrac{U^2_{Đ2}}{P_{Đ2}}=\dfrac{220^2}{75}=\dfrac{1936}{3}\Omega\)
\(R_{tđ}=R_{Đ1}+R_{Đ2}=484+\dfrac{1936}{3}=\dfrac{3388}{3}\Omega\)
\(P=\dfrac{U^2}{R}=\dfrac{220^2}{\dfrac{3388}{3}}=\dfrac{300}{7}W\)
\(R_{ss}=\dfrac{484\cdot\dfrac{1936}{3}}{484+\dfrac{1936}{3}}=\dfrac{1936}{7}\Omega\)
\(P'=\dfrac{U^2}{R}=\dfrac{220^2}{\dfrac{1936}{7}}=175W\)


Điện trở đèn 1: \(R_1=\dfrac{U_1^2}{_1}=\dfrac{220^2}{100}=484\left(\Omega\right)\)
Điện trở đèn 2: \(R_2=\dfrac{U_2^2}{P_2}=\dfrac{220^2}{60}=\dfrac{2420}{3}\left(\Omega\right)\)
\(R_{tđ}=R_1+R_2=484+\dfrac{2420}{3}=\dfrac{3872}{3}\left(\Omega\right)\)
\(I=I_1=I_2=\dfrac{U}{R_{tđ}}=\dfrac{220}{\dfrac{3872}{3}}=\dfrac{15}{88}\left(A\right)\)
\(\left\{{}\begin{matrix}P_1=I^2.R_1=\left(\dfrac{15}{88}\right)^2.484=14,0625\left(W\right)\\P_2=I^2.R_2=\left(\dfrac{15}{88}\right)^2.\dfrac{2420}{3}=23,4375\left(W\right)\end{matrix}\right.\)