Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số trận hòa là a ( a \(\in\)N* )
vì 1 trận hòa là của hai đội,mỗi đội được 1 điểm nên tổng điểm của trận hòa là 2a
theo giả thiết, số trận thắng là 4a
\(\Rightarrow\)tổng số điểm của các trận thắng là 12a
tổng số điểm các đội là 336 \(\Rightarrow\)2a + 12a = 336 \(\Rightarrow\)a = 24
vì vậy có tất cả : 24 + 4.24 = 120 trận đấu
theo giả thiết, có n đội mỗi đội đấu với n-1 đội còn lại nên số trận đấu là : \(\frac{n\left(n-1\right)}{2}\)
suy ra : \(\frac{n\left(n-1\right)}{2}=120\Rightarrow n=16\left(tm\right)\)
Vậy ...

Mỗi đội đấu với 9 đội còn lại, số trận là 9.10/2=45 trận ( do mỗi trận được tính 2 lần).
Gọi số trận thắng thua là x, x≤45, x là số tự nhiên, tổng số điểm thu được là 3x.
Số trận hòa là 45-x, tổng số điểm thu được là 2.(45-x)
Vậy có 3x+2.(45-x)=126 → x=36

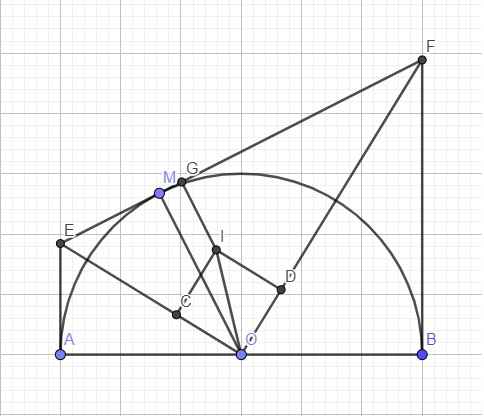
Gọi I là tâm đường tròn nội tiếp EOF, C và D lần lượt là tiếp điểm của (I) với OE và OF
Tứ giác ICOD là hình chữ nhật (có 3 góc vuông)
Mà \(IC=ID=r\Rightarrow ICOD\) là hình vuông
\(S_{IEF}+S_{IEO}+S_{IFO}=\dfrac{1}{2}\left(IG.EF+IC.EO+ID.FO\right)\)
\(=\dfrac{1}{2}r\left(EF+EO+FO\right)\) (do \(IG=IC=ID=r\))
\(=S_{OEF}=\dfrac{1}{2}OM.EF=\dfrac{1}{2}R.EF\)
\(\Rightarrow\dfrac{r}{R}=\dfrac{EF}{EF+OE+OF}>\dfrac{EF}{EF+EF+EF}=\dfrac{1}{3}\)
(do tam giác OEF vuông nên \(OE< EF;OF< EF\))

c) Gọi giao điểm của BM với Ax là I. Từ M kẻ MK vuông góc với AB. BC cắt MK tại E.
Vì MK vuông góc AB => MK // AC // BD
EK // AC => \(\frac{EK}{AC}=\frac{BE}{BC}\); ME // IC => \(\frac{ME}{IC}=\frac{BE}{BC}\) => \(\frac{EK}{AC}=\frac{ME}{IC}\)
Tam giác MIA vuông tại M có CA = CM => góc CAM = góc CMA => góc CIM = góc CMI => tam giác CMI cân tại C => CI = CM => CM = CI = CA => EK = ME.
\(EK=ME\Rightarrow\frac{EK}{BD}=\frac{ME}{BD}\)mà \(\frac{ME}{BD}=\frac{CM}{CD}=\frac{AK}{AB}\Rightarrow\frac{EK}{BD}=\frac{AK}{AB}\)
=> Tam giác AKE đồng dạng với tam giác ABD (c.g.c) => góc EAK = góc DAK => A,E,D thẳng hàng => BC cắt AD tại E mà theo giả thiết BC cắt AD tại N => E trùng với N => H trùng với K => N là trung điểm MH.