Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

𝙁𝙊𝙍
⊂_ヽ 𝙔𝙊𝙐
\\ Λ_Λ
\( ˇωˇ)
> ⌒ヽ
/ へ\
/ / \\𝙋𝘼𝙂𝙀
レ ノ ヽ_つ
/ /
( (ヽ
| |、\
| 丿 \ ⌒)
| | ) /
ノ ) Lノ
(_/

Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không k "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
P/s: Đây là diễn đàn để học, not phải nơi quảng cáo. Oke!
#HuyềnAnh#

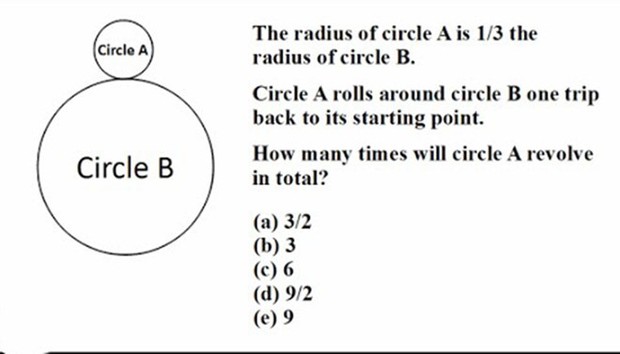
ko có đáp án nào đúng cả chỉ có 1 đáp án ngoài mấy cái đc đưa ra để chọn là 4

a) Gọi bán kính đường tròn (A) là r bán kính đương tròn (B) là 3r. Khi đó:
Chu vi đường tròn (A): \(2r\pi\)
Chu vi đường tròn (B): \(6r\pi\)
=> Chu vi đường tròn B gấp 3 lần chu vi đường tròn A
=> Hình A phải thực hiện 3 vòng quanh B để trở lại điểm xuất phát.

Xem hình cho dễ trả lời nè https://kenh14cdn.com/thumb_w/620/2018/8/31/photo-1-15356853370631011068279.jpg

Giải:
a) Xét \(y'=3x^2+2mx\)
Ta thấy \(y'=3x^2+2mx=0\) có \(\Delta'=m^2>0\forall m\neq 0\) nên luôn có hai nghiệm phân biệt, đồng nghĩa với hàm số đã cho luôn có cực đại, cực tiểu với mọi \(m\neq 0\)
b) Đồ thị hàm số luôn cắt trục hoành tại điểm có hoành độ dương với mọi giá trị của $m$ nghĩa là phương trình \(x^3+mx^2-1=0\) luôn có nghiệm dương với mọi \(m\)
Xét hàm $y$ liên tục trên tập xác định.
Nếu \(m>0\) có \(\left\{\begin{matrix} f(0)=-1<0\\ f(m+1)=(m+1)^3+m(m+1)^2-1>0\end{matrix}\right.\Rightarrow f(0).f(m+1)<0\)
Do đó phương trình luôn có nghiệm thuộc khoảng \((0;m+1)\), tức là nghiệm dương.
Nếu \(m<0\) có \(\left\{\begin{matrix} f(0)=-1<0\\ f(1-m)=m^2-2m>0\forall m<0\end{matrix}\right.\Rightarrow f(0).f(1-m)<0\)
Do đó phương trình luôn có nghiệm thuộc khoảng \((0,1-m)\) , tức nghiệm dương
Từ hai TH ta có đpcm.
c) Để pt có $3$ nghiệm phân biệt thì \(y'=3x^2+2mx\) phải có hai nghiệm phân biệt \(x_1,x_2\) thỏa mãn \(f(x_1)f(x_2)<0\)
Kết hợp với định lý Viete:
\(\Leftrightarrow x_1^3+x_2^3+m(x_1^2+x_2^2)-1>0\)
\(\Leftrightarrow 4m^3-27>0\Leftrightarrow m>\frac{3}{\sqrt[3]{4}}\)