Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(A=-2x^2-10y^2+4xy+4x+4y+2013=-2\left(x-y-1\right)^2-8\left(y-\frac{1}{2}\right)^2+2017\le2017\forall x,y\inℝ\)Đẳng thức xảy ra khi x = 3/2; y = 1/2
2) \(A=a^4-2a^3+2a^2-2a+2=\left(a^2+1\right)\left(a-1\right)^2+1\ge1\)
Đẳng thức xảy ra khi a = 1
3) \(N=\left(x-y\right)\left(x-2y\right)\left(x-3y\right)\left(x-4y\right)+y^4=\left(x^2-5xy+4y^2\right)\left(x^2-5x+6y^2\right)+y^4=\left(x^2-5xy+4y^2\right)^2+2y^2\left(x^2-5xy+4y^2\right)+y^4=\left(x^2-5xy+5y^2\right)^2\)(là số chính phương, đpcm)
4) \(a^3+b^3=3ab-1\Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)-3ab+1=0\Leftrightarrow\left[\left(a+b\right)^3+1\right]-3ab\left(a+b+1\right)=0\)\(\Leftrightarrow\left(a+b+1\right)\left(a^2+2ab+b^2-a-b+1\right)-3ab\left(a+b+1\right)=0\Leftrightarrow\left(a+b+1\right)\left(a^2+b^2-ab-a-b+1\right)=0\)Vì a, b dương nên a + b + 1 > 0 suy ra \(a^2+b^2-ab-a-b+1=0\Leftrightarrow\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2=0\Leftrightarrow a=b=1\)
Do đó \(a^{2018}+b^{2019}=1+1=2\)
5) \(A=n^3+\left(n+1\right)^3+\left(n+2\right)^3=3n\left(n^2+5\right)+9\left(n^2+1\right)⋮9\)(Do số chính phương chia 3 dư 1 hoặc 0)

a)\(=\left(x^2-7x-9x+63\right)+1\)
\(=x^2-7x-9x+63+1\)
=\(x^2-16x+64\)
\(=\left(x-8\right)^2\)
a: \(=x^2-16x+63+1\)
\(=x^2-16x+64=\left(x-8\right)^2\)
b: \(=\left(x^2+x\right)^2-2\left(x^2+x\right)+1+4\left(x^2+x\right)\)
\(=\left(x^2+x\right)^2+2\left(x^2+x\right)+1\)
\(=\left(x^2+x+1\right)^2\)
c: \(=\left(x+2y-3-2\right)^2\)
\(=\left(x+2y-5\right)^2\)
d: \(=\left(x-y\right)^3-1-3\left(x-y\right)^2+3\left(x-y\right)\)
\(=\left(x-y-1\right)^3\)

a)
(x-2y)2 >= 0 V x,y
(y-2018)>=0 V y
=> P=(ghi lại đề) >= 0
vậy GTNN của p bằng 0
dấu "=" xảy ra (=) \(\hept{\begin{cases}x-2y=0\\y-2018=0\end{cases}}\left(=\right)\hept{\begin{cases}x=2y\\y=2018\end{cases}}\left(=\right)\hept{\begin{cases}y=2018\\x=4036\end{cases}}\)
b) (x+y-3)4 >= 0 V x,y
(x-2y)2 >= V x,y
=> Q=(ghi lại đề) >= 2018
vậy GTNN của Q bằng 2018
dấu "=" xảy ra (=) \(\hept{\begin{cases}x+y-3=0\\x-2y=0\end{cases}}\left(=\right)\hept{\begin{cases}x=2y\\3y=3\end{cases}}\left(=\right)\hept{\begin{cases}y=1\\x=2\end{cases}}\)
c)
(2x + 1/6)4>= 0 V x
=> N=(ghi lại đề) >= -2
vậy GTNN của N bằng -2
dấu "=" xảy ra (=) 2x+1/6=0
(=) 2x=-16
(=) x=-1/12
#Học-tốt
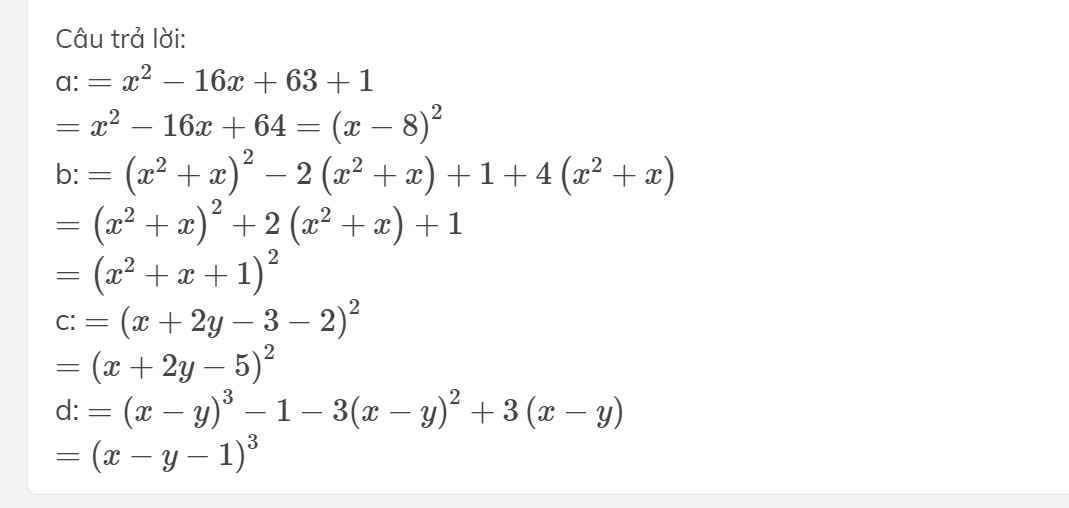
a,\(PT\Leftrightarrow x^2-3x=x^2+2x+1-7\Leftrightarrow-5x=6\Rightarrow x=...\)
b, \(y=4x^2-3\ge-3\)
Do đó y đạt giá trị nhỏ nhất khi x=0.
Mấy câu kia cũng đơn giản mà....dùng HĐT, phân tích thành nhân tử/......cứ thế mà làm..thay đổi chút thôi...