Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AB/DC ( tứ giác ABCD là HBH) => góc ABO = góc CDO ( 2 góc slt)
Ta có: BC//AD ( tứ giác ABCD là HBH) => góc CBO = góc ADO ( 2 góc slt)
Ta có: tứ giác ABCD là HBH => giao điểm O là trung điểm của AC và BD
Xét tam giác AEO và tam giác CFO có:
Góc BAO = góc DCO ( cmt)
OA = OC ( O trung điểm của AC )
góc EOA = góc FOC ( đối đỉnh)
=> tam giác AEO = giác CFO ( c.g.c)
=> EO = FO ( 2 cạnh tương ứng) => O là trung điểm của EF
Xét tam giác BHO = tam giác DGO có:
góc CBO = góc ADO (cmt)
OD = OB ( O là trung điểm của DB )
Góc GOD = góc HOB ( đối đỉnh)
=> tam giác BHO = DGO ( g.c.g)
=> HO = GO ( 2 cạnh tương ứng) => O là trung điểm của GH
Xét tứ giác EGFH
ta có: GH cắt EF tại O
Mà O là trung điểm của EF (cmt)
O là trung điểm của GH (cmt)
=> Tứ giác EGFH là hình bình hành.

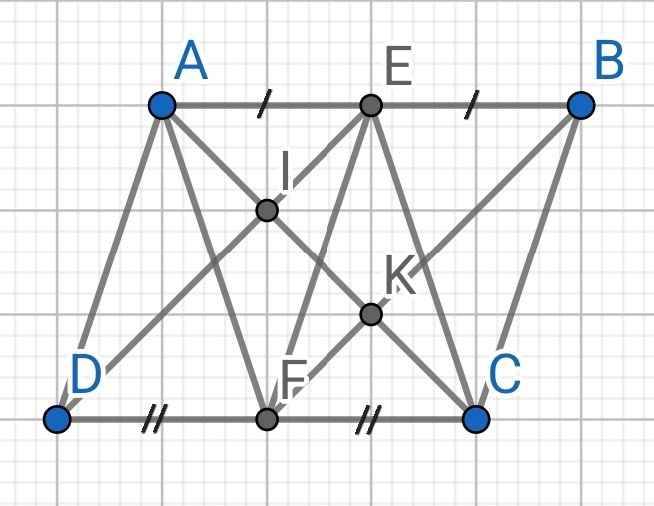 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC

a: Xét tứ giác EBDA có
EB//DA
EA//DB
Do đó: EBDA là hình bình hành
Xét tứ giác ABDF có
AB//DF
AF//BD
Do đó: ABDF là hình bình hành