Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sau thời gian t1 số hạt nhân còn lại là
\(N = N_0 2^{-\frac{t}{T}}\)=> \(\frac{N}{N_0}= 0,2= 2^{-\frac{t_1}{T}}=> t_1 = -T.\ln_20,2.\)
Sau thời điểm t2 thì số hạt nhân còn lại là
\(N_1 = N_0 2^{-\frac{t_2}{T}}=> \frac{N}{N_0} = 0,05 = 2^{-\frac{t_2}{T}}\)=> \(t_2 = -T\ln_20,05.\)
Mà \(t_2 = t_1 +100\)
=> \(-T \ln_2 0,05 = -T\ln_2 0,2 + 100\)
=> \(T = \frac{100}{\ln_2{(0,2/0,05)}}=50 s. \)

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)

Ta để ý rằng số hạt nhân α phát ra cũng chính là số hạt nhân chất phóng xạ bị phân ra
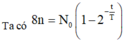
Số hạt nhân ban đầu còn lại sau 414 ngày
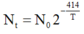
số hạt nhân α đo được trong 1 phút khi đó sẽ là
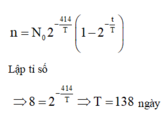
Đáp án B



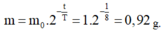
\(X \rightarrow _{-1}^{\ \ 0}e+Y\)
Từ phương trình phóng xạ => Cứ 1 hạt nhân \(X\) bị phóng xạ thì tạo thành 1 hạt nhân \(\beta^-\)
Số hạt nhân \(X\) bị phóng xạ là \(\Delta N = 4,2.10^{13}\) hạt. (1)
Số hạt nhân ban đầu \(X\) (trong 1 gam) là: \(N_0 = \frac{m_0}{A}.N_A= \frac{1}{58,933}.6,023.10^{23} \approx 1,022.10^{22}\)hạt. (2)
Từ (1) và (2) => \(\Delta N = N_0(1-2^{-\frac{t}{T}})\)
=> \(2 ^{-t/T}=1- \frac{\Delta N}{N_0} \)
=> \(\frac{-t}{T} = \ln_2(1- \frac{4,2.10^{13}}{1,022.10^{22}}) =- 5,93.10^{-9}\)
=> \(T \approx 1,68.10^{8}s.\) (\(t = 1s\))
Chọn đáp án.B.1,68.108s.
B