Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo tại đây nhé:
Câu hỏi của KHÔNG CẦN BIẾT - Toán lớp 7 - Học toán với OnlineMath
a, thay m = 3 vào pt ta đc
x2 - ( 2 . 3 +1)x + 2.3 = 0
x2 - 7x + 6 =0
ta có a + b+c= 1 -7 + 6=0
\(\Rightarrow\)pt có 2 nghiệm pb x1 = 1
x2 = 6
b, x2 - (2m +1 )x + 2m=0
\(\Delta\)= [ - (2m + 1 )]2 - 4.2m
= 4m2 + 4m + 1 - 8m
= 4m2 - 4m + 1
= (2m-1)2 \(\ge\)0 \(\forall\)m
để pt có 2 nghiệm pb thì 2m - 1 \(\ne\)0
m \(\ne\)1/2
theo hệ thức vi ét ta có
x1 + x2 = 2m + 1
x1 x2 = 2m
ta có | x1| - |x2| = 2
( |x1| - |x2| )2 = 4
x12 - 2 |x1x2| + x22 =4
x12 + 2 x1x2 + x22 - 2x1x2 - 2 | x1x2| = 4
( x1 + x2)2 - 2 |x1x2| = 4
(2m + 1 )2 - 2|2m|=4 (1 )
+, nếu 2m \(\ge\)0 \(\Rightarrow\)m \(\ge\)0 thì
(1)\(\Leftrightarrow\)(2m + 1)2 - 4m = 4
4m2 + 4m + 1 - 4m = 4
4m2 = 3
m2 = 3/4
\(\Leftrightarrow\orbr{\begin{cases}m=\frac{\sqrt{3}}{2}\left(tm\right)\\m=-\frac{\sqrt{3}}{4}\left(ktm\right)\end{cases}}\)
+, 2m < 0 suy ra m < 0 thì
(1) : (2m + 1 )2 + 4m =4
4m2 + 4m + 1 + 4m = 4
4m2 + 8m - 3 =0
\(\Delta\)= 64 + 4.4.3 = 112 > 0
pt có 2 nghiệm pb x1 = \(\frac{-8+\sqrt{112}}{8}\)= \(\frac{-2+\sqrt{7}}{2}\)(ko tm)
x2 = \(\frac{-2-\sqrt{7}}{2}\)(tm)
vậy m \(\in\){\(\frac{\sqrt{3}}{2}\); \(\frac{-2-\sqrt{7}}{2}\)} thì ...........
ko bt có đúng ko nữa
#mã mã#

a) \(\Delta'=m^2-\left(m-4\right)=m^2-m+4=m^2-2.m.\frac{1}{2}+\frac{1}{4}+\frac{15}{4}\)
\(=\left(m-\frac{1}{2}\right)^2+\frac{15}{4}\ge\frac{15}{4}>0;\forall m\)
=> phương trình (1) luôn có hai nghiệm phân biệt với mọi m
b) Áp dụng định lí Viet ta có:
\(x_1.x_2=m-4\)
\(x_1+x_2=-2m\)
=> \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1.x_2=\left(-2m\right)^2-2\left(m-4\right)=4m^2-2m+8\)
=> \(x_1^3+x_2^3=\left(x_1+x_2\right)\left(x_1^2-x_1x_2+x_2^2\right)=\left(-2m\right)\left(4m^2-2m+8-\left(m-4\right)\right)\)
\(=-2m\left(4m^2-3m+12\right)\)
Theo bài ra ta có:
\(x_1+x_2=\frac{x_1^2}{x_2}+\frac{x_2^2}{x_1}\)
\(\Leftrightarrow x_1+x_2=\frac{x_1^3+x_2^3}{x_1.x_2}\)
Thay vào ta có:
\(-2m=\frac{-2m\left(4m^2-3m+12\right)}{m-4}\)( đk m khác 4)
\(\Leftrightarrow\orbr{\begin{cases}m=0\\m-4=4m^2-3m+12\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m=0\left(tm\right)\\4m^2-4m+16=0\left(l\right)\end{cases}\Leftrightarrow m=0}\)
Vì \(4m^2-4m+16=\left(2m-1\right)^2+15>0\) với mọi m
Vậy m =0
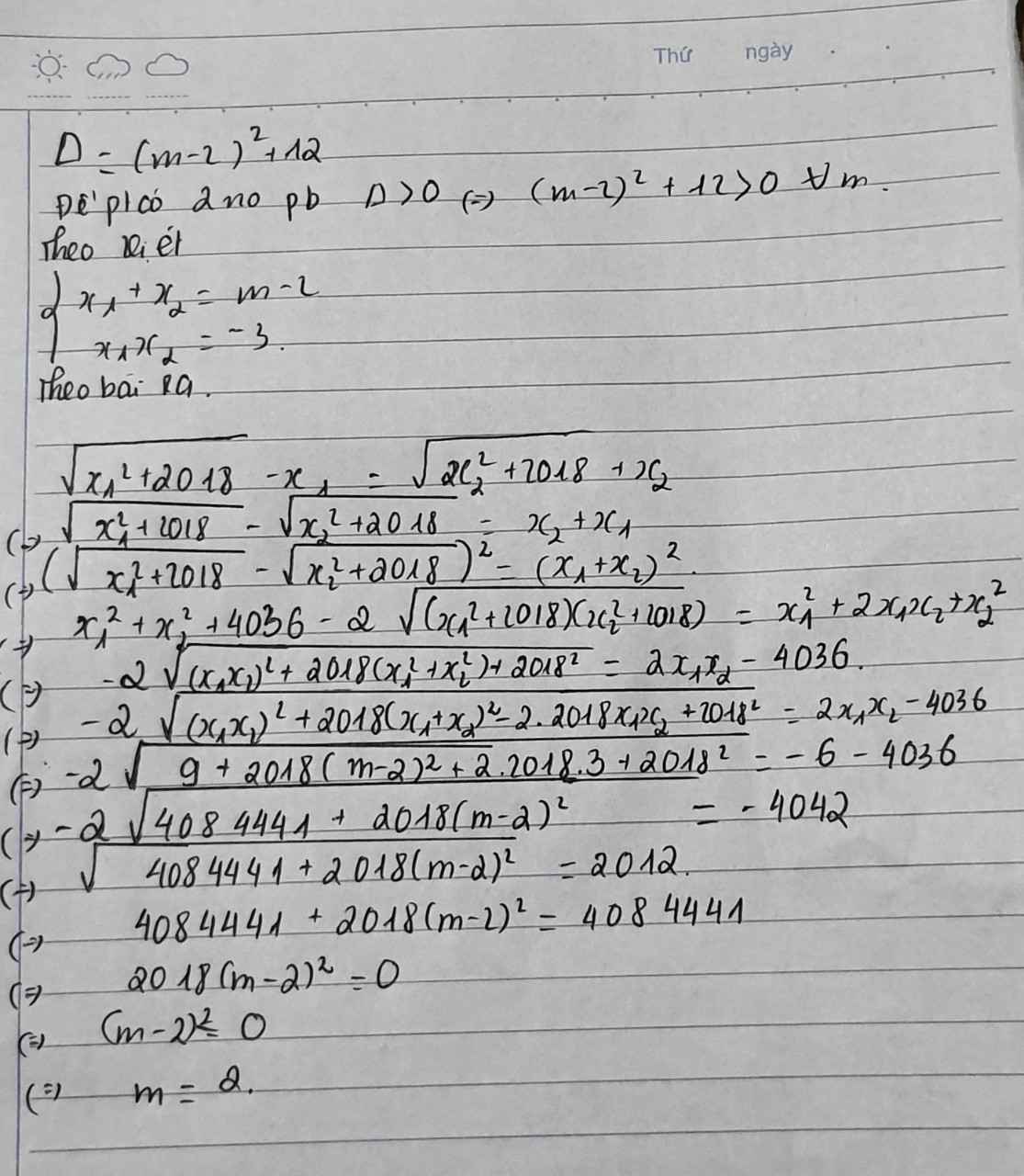
câu b khó hơn đó :v thử r, nó ra bậc 3 lận
Bài 2 :
a,- Để phương trình có 2 nghiệm phân biệt thì : \(\Delta>0\)
<=> \(m^2-4.1.\left(2m-4\right)>0\)
<=> \(m^2-8m+16>0\)
<=> \(\left(m-4\right)^2>0\)
<=> \(m-4>0\)
<=> \(m>4\)
- Nên phương trình có 2 nghiệm phân biệt là :
\(x_1=\frac{m+\sqrt{m-4}}{2},x_2=\frac{m-\sqrt{m-4}}{2}\)
a, Ta có : \(x^2_1+x_2^2=13\)
=> \(\left(\frac{m+\sqrt{m-4}}{2}\right)^2+\left(\frac{m-\sqrt{m-4}}{2}\right)^2=13\)
=> \(\left(m+\sqrt{m-4}\right)^2+\left(m-\sqrt{m-4}\right)^2=52\)
=> \(m^2+2m\sqrt{m-4}+m-4+m^2-2m\sqrt{m-4}+m-4-52=0\)
=> \(2m^2+2m-60=0\)
=> \(m^2+m-30=0\)
=> \(m^2+\frac{m.2.1}{2}+\frac{1}{4}=30+\frac{1}{4}=\frac{121}{4}\)
=> \(\left(m+\frac{1}{2}\right)^2=\frac{121}{4}\)
=> \(\left[{}\begin{matrix}m=\sqrt{\frac{121}{4}}-\frac{1}{2}=5\left(TM\right)\\m=-\sqrt{\frac{121}{4}}-\frac{1}{2}=-6\left(KTM\right)\end{matrix}\right.\)
Vậy m có giá trị bằng 5 thỏa mãn điều kiện .
b, Làm tương tự nha .