Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}2x-\left(m^2+m+1\right)y=-m^2-9\left(1\right)\\m^4x+\left(2m^2+1\right)y=1\left(2\right)\end{matrix}\right.\)
rút x từ (1) thế vào (2)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\left(m^2+m+1\right)y-m^2-9}{2}\left(3\right)\\m^4\left[\dfrac{\left(m^2+m+1\right)y-m^2-9}{2}\right]+\left(2m^2+1\right)y=1\left(4\right)\end{matrix}\right.\)
\(\left(4\right)\Leftrightarrow m^4\left(m^2+m+1\right)y-m^4\left(m^2+9\right)+2\left(2m^2+1\right)y=2\)
\(\Leftrightarrow\left[m^4\left(m^2+m+1\right)+4m^2+2\right]y=m^4\left(m^2+9\right)+2\)
\(\Leftrightarrow Ay=B\)
Taco
\(\left\{{}\begin{matrix}m^2+m+1=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall m\in R\\4m^2+2>0\forall m\in R\\m^4\left(m^2+9\right)>0\forall m\in R\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A>0\forall m\in R\\B>0\forall m\in R\end{matrix}\right.\)
\(\Rightarrow y>0\forall m\in R\)
Kết luận không có m thủa mãn

1. \(\left\{{}\begin{matrix}x+y+\dfrac{1}{x}+\dfrac{1}{y}=5\\x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=9\end{matrix}\right.\) ĐKXĐ : \(\left\{{}\begin{matrix}x>0\\y>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2y+xy^2+x+y=5xy\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^4y^2+x^2y^4+x^2+y^2=25x^2y^2\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\)\(\Leftrightarrow0=16x^2y^2\)
\(\Rightarrow\) phương trình vô nghiệm

1.
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2-2m\left(x+\dfrac{1}{x}\right)-1+2m=0\)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow\left|t\right|\ge2\)
\(\Rightarrow t^2-1-2mt+2m=0\)
\(\Leftrightarrow\left(t-1\right)\left(t+1\right)-2m\left(t-1\right)=0\)
\(\Leftrightarrow\left(t-1\right)\left(t+1-2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=1\left(loại\right)\\t=2m-1\end{matrix}\right.\)
Pt có nghiệm \(\Leftrightarrow\left[{}\begin{matrix}2m-1\ge2\\2m-1\le-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge\dfrac{3}{2}\\m\le-\dfrac{1}{2}\end{matrix}\right.\)
2.
Cộng vế với vế: \(3\left|x\right|=3\Rightarrow\left|x\right|=1\)
\(\Rightarrow\left|y\right|=-1< 0\) (không thỏa mãn)
Vậy hệ pt vô nghiệm

a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
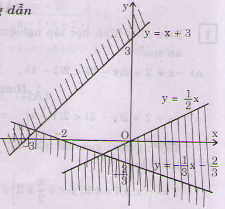
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
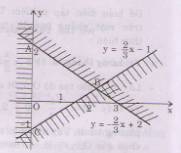

a: \(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y}=5\\\dfrac{1}{x}-\dfrac{4}{y}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y}=5\\\dfrac{2}{x}-\dfrac{8}{y}=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{y}=11\\\dfrac{1}{x}-\dfrac{4}{y}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\\dfrac{1}{x}=-3+\dfrac{4}{y}=-3+4=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{12}{x-3}-\dfrac{5}{y+2}=63\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{36}{x-3}-\dfrac{15}{y+2}=189\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{44}{x-3}=176\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3=\dfrac{1}{4}\\\dfrac{15}{y+2}=-13-\dfrac{8}{x-3}=-13-32=-45\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{13}{4}\\y=-\dfrac{1}{3}-2=-\dfrac{7}{3}\end{matrix}\right.\)

Áp dụng bđt AM-GM có:
\(1+\dfrac{y}{z}\ge2\sqrt{\dfrac{y}{z}};1+\dfrac{z}{x}\ge2\sqrt{\dfrac{z}{x}}\)
Dễ dàng suy ra: \(M\ge\dfrac{x}{y}+2\sqrt{2}\cdot\sqrt[4]{\dfrac{y}{z}}+3\sqrt[3]{2}\cdot\sqrt[6]{\dfrac{z}{x}}=\dfrac{1}{\sqrt{2}}\left(\dfrac{x}{y}+4\sqrt[4]{\dfrac{y}{z}}+6\sqrt[6]{\dfrac{z}{x}}\right)+\left(1-\dfrac{1}{\sqrt{2}}\right)\cdot\dfrac{x}{y}+\left(3\sqrt[3]{2}-3\sqrt{2}\right)\cdot\sqrt[6]{\dfrac{z}{x}}\)
Theo AM-GM có: \(\dfrac{1}{\sqrt{2}}\left(\dfrac{x}{y}+4\sqrt[4]{\dfrac{y}{z}}+6\sqrt[6]{\dfrac{z}{x}}\right)\ge\dfrac{1}{2}\cdot11\sqrt[11]{\dfrac{x}{y}\cdot\dfrac{y}{z}\cdot\dfrac{z}{x}}=\dfrac{11}{\sqrt{2}}\) (1)
Theo đề: \(x\ge max\left\{y,z\right\}\) ta có: \(\left\{{}\begin{matrix}\dfrac{x}{y}\ge1\\\dfrac{z}{x}\le1\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}\left(1-\dfrac{1}{\sqrt{2}}\right)\cdot\dfrac{x}{y}\ge1-\dfrac{1}{\sqrt{2}}\left(2\right)\\\left(3\sqrt[3]{2}-3\sqrt{2}\right)\cdot\sqrt[6]{\dfrac{z}{x}}\ge3\sqrt[3]{2}-3\sqrt{2}\left(3\right)\end{matrix}\right.\)
Cộng theo vế bđt (1), (2) ,(3) có:\(A\ge\dfrac{11}{\sqrt{2}}+1-\dfrac{1}{\sqrt{2}}+3\sqrt[3]{2}-3\sqrt{2}=1+2\sqrt{2}+3\sqrt[3]{2}\)
Xảy ra khi \(x=y=z\)
Lâu lâu k đi khủng bố tinh thần :3
Ta đi cm \(1+2\sqrt{2}+3\sqrt[3]{2}\) là Min nhé
\(M'(x)=\dfrac{1}{y}+\dfrac{-\dfrac{z}{x^2}}{\sqrt[3]{\left(1+\dfrac{z}{x}\right)^2}}=\dfrac{x^2\sqrt[3]{\left(1+\dfrac{z}{x}\right)^2}-yz}{y\sqrt[3]{\left(1+\dfrac{z}{x}\right)^2}}\ge0\)
Vì vậy ta cần xét 2 trường hợp
*)\(y\ge z;x=y\). Đặt \(\dfrac{y}{z}=t\). Khi đó \(t\ge 1\) và cần cm \(f(t)\ge 0\)
\(f(t)=2\sqrt{1+t}+3\sqrt[3]{1+\dfrac{1}{t}}-2\sqrt{2}-3\sqrt[3]{2}\)
Thật vậy \(f'(t)=\dfrac{1}{\sqrt{1+t}}+\dfrac{-\dfrac{1}{t^2}}{\sqrt[3]{1+\dfrac{1}{t}}}=\dfrac{\sqrt[3]{t^4(t+1)^2}-\sqrt{1+t}}{\sqrt{1+t}\sqrt[3]{t^4(t+1)^2}}>0\)
\(\Rightarrow f(t)\ge f(1)=0\)
*)\(z\ge y ;x=z\). Khi đó \(t\ge 1\) và ta cm \(g(t)\ge 0\)
\(g(t)=t+2\sqrt{1+\dfrac{1}{t}}-1-2\sqrt{2}\)
Và \(g'(t)=1+\dfrac{-\dfrac{1}{t^2}}{\sqrt{1+\dfrac{1}{t}}}=\dfrac{\sqrt{t^3(t+1)}-1}{\sqrt{t^3(t+1)}}>0\)
Tức là \(g(t)\geq g(1)=0\)

Câu 1:
\(\Leftrightarrow\left\{{}\begin{matrix}13x>\dfrac{7}{3}\\4x-16< 3x-14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{7}{39}\\x< 2\end{matrix}\right.\Leftrightarrow\dfrac{7}{39}< x< 2\)
mà x nguyên
nên x=1
Câu 2:
\(\Leftrightarrow\left\{{}\begin{matrix}2x< 4\\mx>2-m\end{matrix}\right.\)
=>x<2 và mx>2-m
Nếu m=0 thì bất phươg trình vô nghiệm
Nếu m<>0 thì BPT sẽ tương đương với:
\(\left\{{}\begin{matrix}x< 2\\x>\dfrac{2-m}{m}\end{matrix}\right.\)
Để BPT vô nghiệm thì 2-m/m>=2
=>\(\dfrac{2-m}{m}-2>=0\)
=>\(\dfrac{2-m-2m}{m}>=0\)
=>\(\dfrac{3m-2}{m}< =0\)
=>0<m<=2/3