Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gia tốc vật:
\(a=\dfrac{F_k}{m}=\dfrac{4}{2}=2\)m/s2
Sau khi đi được 9m thì vật đạt vận tốc:
\(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS+v^2_0}=\sqrt{2\cdot2\cdot9+0^2}=6\)m/s

Chọn A
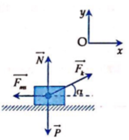
Vật chịu tác dụng của trọng lực P → , phản lực N → của mặt đường, lực kéo F K → và lực ma sát trượt . Chọn hệ trục Oxy như hình vẽ.
Áp dụng định luật II Niu-ton:
Chiếu lên trục Oy:
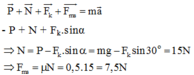
Chiếu lên trục Ox:
![]()
v = a.t = 0,58.5 = 2,9 m/s.

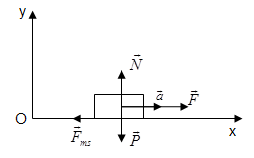
- Các lực tác dụng lên vật: Lực kéo \(\overrightarrow{F}\), lực ma sát\(\overrightarrow{F_{ms}}\), trọng lực \(\overrightarrow{P}\), phản lực \(\overrightarrow{N}\)
- Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên.
- Phương trình định luật II Niu-tơn dưới dạng véc tơ:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\left(1\right)\)
- Chiếu (1) lên trục Ox, Oy ta được:
\(\hept{\begin{cases}F-F_{ms}=m.a\\-P+N=0\end{cases}\Rightarrow\hept{\begin{cases}a=\frac{F-F_{ms}}{m}\\P=N\end{cases}}}\)
Có: \(F_{ms=\mu_t.N=\mu_t.P=\mu_t.mg}\)
→ Gia tốc chuyển động của vật: \(a=\frac{F-F_{ms}}{m}=\frac{F-\mu_t.mg}{m}\)

Chọn A
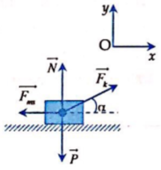
Vật chịu tác dụng của trọng lực P ⇀ , phản lực N ⇀ của mặt đường, lực kéo F k ⇀ và lực ma sát trượt F m s ⇀ . Chọn hệ trục Oxy như hình vẽ.
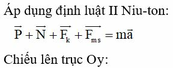
− P + N + F k . sin α = 0
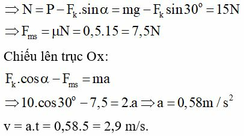

m=8kg
Fk=24N
v0 =0
μ=0,2; g =10m/s2
a) Lực ma sát có độ lớn là :
\(F_{ms}=\mu N=\mu mg=0,2.8.10=16\left(N\right)\)
Ta có : \(F=F_k-F_{ms}=24-16=8\left(N\right)\)
Mà : F=ma => a=\(\frac{F}{a}=\frac{8}{8}=1\left(m/s^2\right)\)
b) V1 =72km/h=20m/s
=> \(s=\frac{20^2-0^2}{2.1}=200\left(m\right)\)
Gia tốc vật:
\(a=\dfrac{F_k}{m}=\dfrac{4}{2}=2\)m/s2
Sau khi đi được 9m kể từ lúc bắt đầu \(\left(v_0=0\right)\) thì vật đạt vận tốc: \(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS}=\sqrt{2\cdot2\cdot9}=6\)m/s