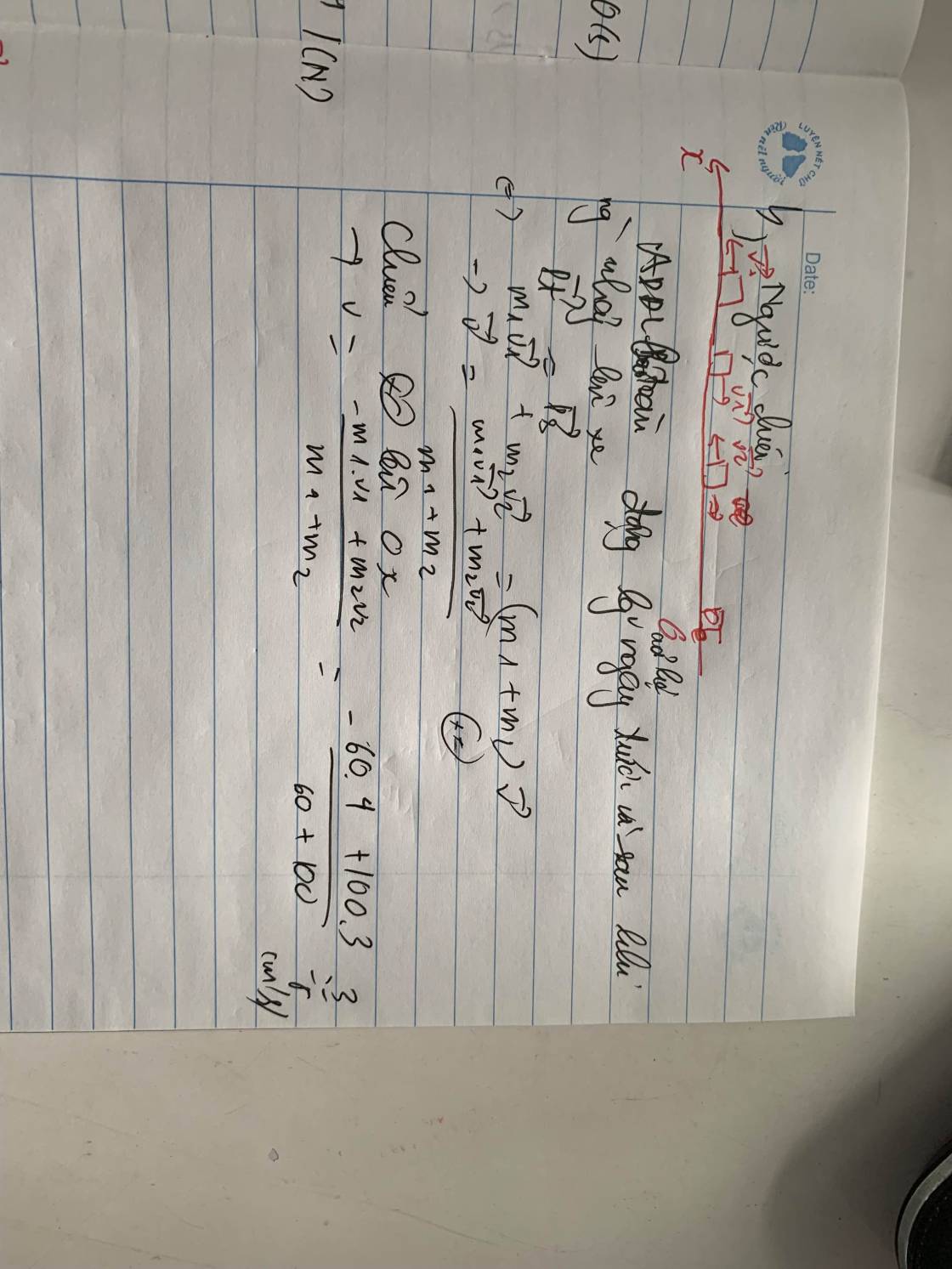Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định luật bảo toàn động lượng :
→pt=→ps��→=��→ <=> m1→v1=m2→v2�1�1→=�2�2→
=> m1→v1+m2→v2=→v(m1+m2)�1�1→+�2�2→=�→(�1+�2)
<=> →v=m1→v1+m2→v2m1+m2�→=�1�1→+�2�2→�1+�2
chọn chiều dương là chiều chuyển động ban đầu của xe
a)Cùng chiều : v=60.4+3.10060+90=3,6(m/s)�=60.4+3.9060+90=3,4(�/�)
b) Ngược chiều : v=−60.4+3.10060+90=0,4(m/s)

Chọn chiều chuyển động ban đầu của xe cát là chiều dương. Hệ vật gồm xe cát và vật nhỏ chuyển động theo cùng phương ngang, nên có thể biểu diễn tổng động lượng của hệ vật này dưới dạng tổng đại số.
Trước khi vật xuyên vào xe cát: p 0 = M V 0 + m v 0
Sau khi vật xuyên vào xe cát: p = (M + m)V.
Áp dụng định luật bảo toàn động lượng, ta có :
p = p 0 ⇒ (M + m)V = M V 0 + m v 0
Suy ra : V = (M V 0 + m v 0 )/(M + m)
Khi vật bay đến ngược chiều chuyển động của xe cát, thì v 0 = -6 m/s, nên ta có :
V = (98.1 + 2.(-6))/(98 + 2) = 0,86(m/s)

Chọn chiều chuyển động ban đầu của xe cát là chiều dương. Hệ vật gồm xe cát và vật nhỏ chuyển động theo cùng phương ngang, nên có thể biểu diễn tổng động lượng của hệ vật này dưới dạng tổng đại số.
Trước khi vật xuyên vào xe cát: p 0 = M V 0 + m v 0
Sau khi vật xuyên vào xe cát: p = (M + m)V.
Áp dụng định luật bảo toàn động lượng, ta có :
p = p 0 ⇒ (M + m)V = M V 0 + m v 0
Suy ra : V = (M V 0 + m v 0 )/(M + m)
Khi vật bay đến cùng chiều chuyển động của xe cát, thì v 0 = 7 m/s, nên ta có :
V = (98.1 + 2.6)/(98 + 2) = 1,1(m/s)

Lời giải
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của viên đạn
Gọi v 1 , v 2 , V lần lượt là vận tốc viên đạn, xe lúc trước là xe lúc sau va chạm. Ta có:
m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 ⇔ 7 , 4 = m 1 .600 − 1 , 5.0 , 5 m 1 + 1 , 5 ⇔ m 1 = 0 , 02 k g = 20 g
Với v 2 = − 0 , 5 m / s vì xe chuyển động ngược chiều so với viên đạn
Đáp án: A

a)Qũy đạo của hòn đá: \(y=25+v_0sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
Thời gian chuyển động của hòn đá:
\(\Rightarrow0=25+v_0\cdot sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
\(\Rightarrow0=25+15\cdot sin30\cdot t-\dfrac{1}{2}\cdot10\cdot t^2\)
\(\Rightarrow t\approx3,11s\)
b)Khoảng cách từ chân tháp đến chỗ rơi:
\(S=x=v_0\cdot cos\alpha\cdot t\)
\(\Rightarrow S=15\cdot sin30\cdot3,11=23,325m\)
c)Ta có: \(v_x=v_0\cdot cos\alpha\)
\(v_y=v_0\cdot sin\alpha-gt\)
Vận tốc hòn đá lúc chạm đất:
\(v=\sqrt{(v_0\cdot sin\alpha)^2+\left(v_0\cdot sin\alpha-gt\right)^2}\)
\(=\sqrt{\left(15\cdot sin30\right)^2+\left(15\cdot sin30-10\cdot3,1\right)^2}\)
\(\approx24,7\)m/s
ở trên cho vx=v0⋅cosα sao xuống dưới chuyển thành sin rồi, v của bài này là 26,94 m/s ấy.

Bài 1 :
P1 =m1g => m1 = 1(kg)
P2 = m2g => m2 =1,5(kg)
Trước khi nổ, hai mảnh của quả lựu đạn đều chuyển động với vận tốc v0, nên hệ vật có tổng động lượng : \(p_0=\left(m_1+m_2\right)v_0\)
Theo đl bảo toàn động lượng : \(p=p_0\Leftrightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v_0\)
=> \(v_1=\frac{\left(m_1+m_2\right)v_0-m_2v_2}{m_1}=\frac{\left(1+1,5\right).10-1,5.25}{1}=-12,5\left(m/s\right)\)
=> vận tốc v1 của mảnh nhỏ ngược hướng với vận tốc ban đầu v0 của quả lựu đạn.
Bài2;
Vận tốc mảnh nhỏ trước khi nổ là :
v02=\(v_1^2=2gh\)
=> v1 = \(\sqrt{v_0^2-2gh}=\sqrt{100^2-2.10.125}=50\sqrt{3}\left(m/s\right)\)
Theo định luật bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
p = mv = 5.50 =250(kg.m/s)
\(\left\{{}\begin{matrix}p_1=m_1v_1=2.50\sqrt{3}=100\sqrt{3}\left(kg.m/s\right)\\p_2=m_2v_2=3.v_2\left(kg.m/s\right)\end{matrix}\right.\)
+ Vì \(\overrightarrow{v_1}\perp\overrightarrow{v_2}\rightarrow\overrightarrow{p_1}\perp\overrightarrow{p_2}\)
=> p2 = \(\sqrt{p_1^2+p^2}=\sqrt{\left(100\sqrt{3}\right)^2+250^2}=50\sqrt{37}\left(kg.m/s\right)\)
=> v2= \(\frac{p_2}{m_2}=\frac{50\sqrt{37}}{3}\approx101,4m/s+sin\alpha=\frac{p_1}{p_2}=\frac{100\sqrt{3}}{50\sqrt{3}}\)
=> \(\alpha=34,72^o\)