Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số mũ: y = a x
- Tập xác định: D = R.
- Chiều biến thiên:
+ y = a x .lna
a > 1 ⇒ y’ > 0 ⇒ Hàm số đồng biến trên R.
0 < a < 1 ⇒ y’ < 0 ⇒ Hàm số nghịch biến trên R.
+ Tiệm cận: 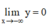
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
- Đồ thị:
+ Đồ thị đi qua (0; 1) và (1; a).
+ Đồ thị nằm phía trên trục hoành.

1. Hàm số mũ
Cho số a > 0 và a ≠ 1. Hàm số y = a x được gọi là hàm số mũ cơ số a.
Các tính chất của hàm số mũ y = a x
| Tập xác định | (-∞; +∞) |
| Đạo hàm | y’= a x .lna |
| Chiều biến thiên | + Nếu a > 1 thì hàm số luôn đồng biến + Nếu 0 < a < 1 thì hàm số nghịch biến |
| Tiệm cận | Trục Ox là tiệm cận ngang |
| Đồ thị | Đi qua các điểm (0; 1); (1; a) Nằm phía trên trục hoành ( y = a x > 0 mọi x) |
2. Hàm Logarit
Cho số a > 0 và a ≠ 1 . Hàm số y = logax được gọi là hàm số logarit cơ số a
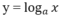
| Tập xác định | (0; +∞) |
| Đạo hàm |  |
| Chiều biến thiên | + Nếu a > 1: hàm số luôn đồng biến + Nếu 0 < a < 1: hàm số luôn nghịch biến |
| Tiệm cận | Trục Oy là tiệm cận đứng |
| Đồ thị | Đi qua các điểm (1; 0); (a; 1) Nằm bên phải trục tung. |
3. Liên hệ giữa đồ thị của hàm số mũ và hàm số logarit cùng cơ số: Đồ thị của hàm số mũ và đồ thị của hàm số logarit đối xứng nhau qua đường phân giác góc phần tư thứ nhất.

1. Hàm số mũ
Cho số a > 0 và a ≠ 1. Hàm số y = ax được gọi là hàm số mũ cơ số a.
Các tính chất của hàm số mũ y = ax
Tập xác định | (-∞; +∞) |
Đạo hàm | y’= ax.lna |
Chiều biến thiên | + Nếu a > 1 thì hàm số luôn đồng biến + Nếu 0 < a < 1 thì hàm số nghịch biến |
Tiệm cận | Trục Ox là tiệm cận ngang |
Đồ thị | Đi qua các điểm (0; 1); (1; a) Nằm phía trên trục hoành ( y = ax > 0 mọi x) |
2. Hàm Logarit
Cho số a > 0 và a ≠ 1 . Hàm số y = logax được gọi là hàm số logarit cơ số a
| Tập xác định | (0; +\(\infty\)) |
| Đạo hàm | y' = \(\frac{1}{xIna}\) |
| Chiều biến thiên | + Nếu a > 1: hàm số luôn đồng biến + Nếu 0 < a < 1: hàm số luôn nghịch biến |
| Tiệm cận | Trục Oy là tiệm cận đứng |
| Đồ thị | Đi qua các điểm (1; 0); (a; 1) Nằm bên phải trục tung. |
3. Liên hệ giữa đồ thị của hàm số mũ và hàm số logarit cùng cơ số: Đồ thị của hàm số mũ và đồ thị của hàm số logarit đối xứng nhau qua đường phân giác góc phần tư thứ nhất.
HT

- Tính chất của hàm số mũ y= ax ( a > 0, a# 1).
- Tập xác định: .
- Đạo hàm: ∀x ∈ ,y’= axlna.
- Chiều biến thiên Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
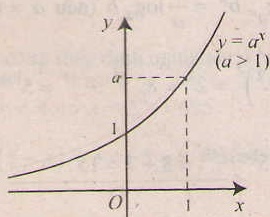
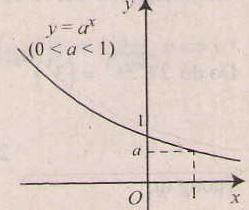
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành ( y= ax > 0, ∀x), và luôn cắt trục tung taih điểm ( 0;1) và đi qua điểm (1;a).
- Tính chất của hàm số lôgarit y = logax (a> 0, a# 1).
- Tập xác định: (0; +∞).
- Đạo hàm ∀x ∈ (0; +∞),y’ = .
- Chiều biến thiên: Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
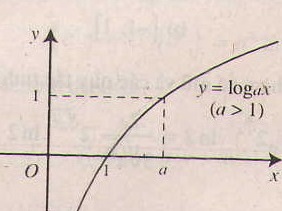
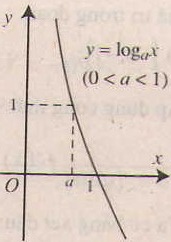

1. Tính chất của hàm số mũ y= ax ( a > 0, a# 1).
- Tập xác định: .
- Đạo hàm: ∀x ∈ ,y’= axlna.
- Chiều biến thiên Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
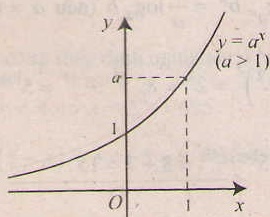
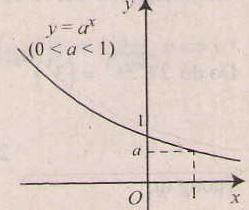
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành ( y= ax > 0, ∀x), và luôn cắt trục tung taih điểm ( 0;1) và đi qua điểm (1;a).
2. Tính chất của hàm số lôgarit y = logax (a> 0, a# 1).
- Tập xác định: (0; +∞).
- Đạo hàm ∀x ∈ (0; +∞),y’ = .
- Chiều biến thiên: Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
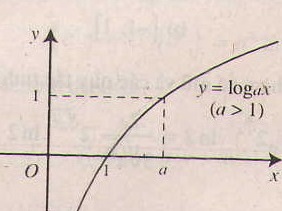
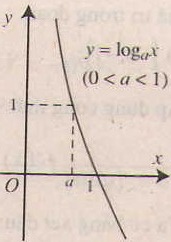
3. Chú ý
- Vì e > 1 nên nếu a > 1 thì lna > 0, suy ra (ax)’ > 0,∀x và (logax)’ > 0, ∀x > 0;
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu 0 < a< 1thì lna < 0, (ax)’ < 0 và (logax)’ < 0, ∀x > 0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành
(ln|x|)’ = , ∀x # 0 và (loga|x|)’ =
, ∀x # 0.
Cái này bạn hoàn toàn có thể xem ở sách giáo khoa được mà?