
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:\(P=\left(1-\dfrac{1}{1+2}\right)\left(1-\dfrac{1}{1+2+3}\right)...\left(1-\dfrac{1}{1+2+...+2014}\right)\)
\(P=\dfrac{2}{1+2}\cdot\dfrac{2+3}{1+2+3}\cdot...\cdot\dfrac{2+3+...+2014}{1+2+3+...+2014}\)
\(P=\dfrac{\dfrac{1\cdot4}{2}}{\dfrac{2\left(2+1\right)}{2}}\cdot\dfrac{\dfrac{2\left(3+2\right)}{2}}{\dfrac{3\left(3+1\right)}{2}}\cdot...\cdot\dfrac{\dfrac{2013\left(2014+2\right)}{2}}{\dfrac{2014\left(2014+1\right)}{2}}\)
\(P=\dfrac{1\cdot4}{2\cdot3}\cdot\dfrac{2\cdot5}{3\cdot4}\cdot...\cdot\dfrac{2013\cdot2016}{2014\cdot2015}\)
\(P=\dfrac{1\cdot4\cdot2\cdot5\cdot...\cdot2013\cdot2016}{2\cdot3\cdot3\cdot4\cdot...\cdot2014\cdot2015}\)
\(P=\dfrac{\left(1\cdot2\cdot...\cdot2013\right)\left(4\cdot5\cdot...\cdot2016\right)}{\left(2\cdot3\cdot\cdot...\cdot2014\right)\left(3\cdot4\cdot...\cdot2015\right)}\)
\(P=\dfrac{2016}{2014\cdot3}\)
\(P=\dfrac{336}{1007}\)

1)\(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}\)
\(A< \dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{99.100}\)
\(A< \dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A< \dfrac{1}{4}-\dfrac{1}{100}\)
\(A< \dfrac{1}{4}\)(1)
\(A>\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{100.101}\)
\(A>\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{100}-\dfrac{1}{101}\)
\(A>\dfrac{1}{5}-\dfrac{1}{101}\)
\(A>\dfrac{96}{505}>\dfrac{1}{6}\)
\(A>\dfrac{1}{6}\)(2)
Từ (1) và (2)
\(\dfrac{1}{6}< A< \dfrac{1}{4}\)
2)
\(A=\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+...+\dfrac{1}{92.95}+\dfrac{1}{95.98}\)
\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{92}-\dfrac{1}{95}+\dfrac{1}{95}-\dfrac{1}{98}\right)\)\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{98}\right)\)
\(A=\dfrac{1}{3}.\dfrac{24}{49}=\dfrac{8}{49}\)

1.Kết quả phép tính36.34.32 là:
A.272 B.312 C.348 D.30
2.Từ tỉ lệ thức \(\frac{a}{b}\)=\(\frac{c}{d}\)(a,b,c,d #0) ta có thể suy ra:
A.\(\frac{d}{b}\)=\(\frac{c}{a}\) B.\(\frac{a}{b}\)=\(\frac{c}{d}\)
C.\(\frac{a}{c}\)=\(\frac{d}{b}\) D.\(\frac{a}{d}\)=\(\frac{b}{c}\)
3.Nếu\(\sqrt{x}\)=4 thì x bằng:
A.\(\pm\)2 B.\(\pm\)6 C.\(\pm\)2 D.\(\pm\)16
Hok tốt!


\(\frac{1}{2}a=\frac{2}{3}b=\frac{3}{4}c\)
\(\Leftrightarrow\)\(\frac{a}{12}=\frac{b}{9}=\frac{c}{8}\)
Ap dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{12}=\frac{b}{9}=\frac{c}{8}=\frac{a-b}{12-9}=\frac{15}{3}=5\)
suy ra \(\hept{\begin{cases}\frac{a}{12}=5\\\frac{b}{9}=5\\\frac{c}{8}=5\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}a=60\\b=45\\c=40\end{cases}}\)
Vậy.....
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{2b}{3}=\frac{3c}{4}=\frac{a}{2}=\frac{b}{\frac{3}{2}}=\frac{3c}{4}=\frac{a-b}{2-\frac{3}{2}}=\frac{15}{\frac{1}{2}}=30\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{a}{2}=30\Rightarrow a=60\\\frac{2b}{3}=30\Rightarrow b=45\\\frac{3c}{4}=30\Rightarrow c=40\end{cases}}\)



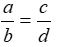 (a, b, c, d # 0) ta có thể suy ra:
(a, b, c, d # 0) ta có thể suy ra: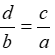 B.
B. 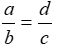
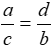 D.
D.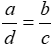
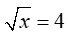 thì x bằng:
thì x bằng: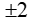 B.
B. 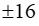 C. 2 D.16
C. 2 D.16
KHI ĐÓ THAY a=1,b=2,c=3 LÀ ĐƯỢC
MÌNH LÀM VẬY ĐÚNG
vío lai thay =1,2,3