Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Xét ΔADO vuông tại D và ΔAEO vuông tại E có
AO chung
\(\widehat{DAO}=\widehat{EAO}\)
Do đó: ΔADO=ΔAEO
Suy ra: OD=OE
Bài 3:
Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD

Giải
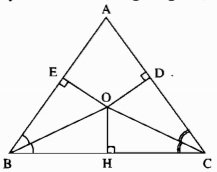
Kẻ OH⊥BC
Xét hai tam giác vuông OEB và OHB, ta có:
\(\widehat{\text{OEB}}=\widehat{\text{OHB}}\)=90o
Cạnh huyền OB chung
\(\widehat{EBO}=\widehat{\text{HB}O}\)(gt)
Suy ra: ∆OEB = ∆OHB (cạnh huyền, góc nhọn)
⇒ OE = OH (hai cạnh tương ứng) (1)
Xét hai tam giác vuông OHC và ODC, ta có:
\(\widehat{\text{OHC}}=\widehat{\text{ODC}}\)=90oCạnh huyền OC chung
\(\widehat{\text{HCO}}=\widehat{\text{DCO}}\)(gt)
Suy ra: ∆OHC = ∆ODC (cạnh huyền, góc nhọn)
⇒ OH = OD (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: OE = OD.

Ta có hình vẽ:ABCOEDXét tam giác EOB và tam giác DOC có:
\(\widehat{E}\)=\(\widehat{D}\)=900
\(\widehat{EBO}\)=\(\widehat{DCO}\)
OB = OC
=> tam giác EOB = tam giác DOC
=> OD = OE (2 cạnh tương ứng)

a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.

A B H M C E D
a) Xét \(\Delta ABC\)cân tại A có AM là trung tuyến \(\Rightarrow\)M là trung điểm BC
\(\Rightarrow MB=MC\)
Xét \(\Delta MDC\)và \(\Delta MHB\)có: +) \(\widehat{BHM}=\widehat{CDM}=90^o\)
+) \(MB=MC\)
+) \(\widehat{BMH}=\widehat{CMD}\)( đối đỉnh )
\(\Rightarrow\Delta MDC=\Delta MHB\)( cạnh huyền - góc nhọn ) ( đpcm )
b) Từ \(\Delta MDC=\Delta MHB\)\(\Rightarrow\widehat{C}=\widehat{MBH}\)( 2 góc tương ứng )
mà \(\widehat{C}=\widehat{ABC}\)( \(\Delta ABC\)cân tại A ) \(\Rightarrow\widehat{ABC}=\widehat{MBH}\)
Xét \(\Delta BME\)và \(\Delta BMH\)có: +) \(\widehat{BEM}=\widehat{BHM}=90^o\)
+) chung cạnh MB
+) \(\widehat{ABC}=\widehat{HBC}\)
\(\Rightarrow\Delta BME=\Delta BMH\)( cạnh huyền - góc nhọn )
\(\Rightarrow ME=MH\)( 2 cạnh tương ứng ) \(\Rightarrow\Delta EMH\)cân tại M ( đpcm )
A B C O D E
Nối OA. Vì O là giao điểm của hai đường phân giác BO và CO nên O đường phân giác thứ ba cũng đi qua O. Suy ra OA là tia phân giác của góc A. Xét hai tam giác vuông : tam giác AOD và tam giác AOE có AO là cạnh chung , góc BOA = góc OAD
=> tam giác AEO = tam giác ADO (ch.gn) => OD = OE
Lưu ý: Các bạn vẽ hình nữa nha