Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

R1 nt R2: Rtđ = U2/P = 122/5,76 = 25 Ω
\(\Leftrightarrow\) R1 + R2 = 25 Ω (1)
R1 // R2: R'tđ = U2/P' = 122 /24 = 6 Ω
\(\Leftrightarrow\) R1.R2 / R1 + R2 = 6 Ω
\(\Leftrightarrow\) R1.R2 / 25 = 6
\(\Leftrightarrow\) R1. R2 = 25.6 = 150 Ω (2)
Từ (1) và (2)
\(\Rightarrow\) R1 = 15 Ω ; R2 = 10 Ω
hoặc
R1 = 10 Ω; R2 = 15Ω

Bài 2 :
Tóm tắt :
\(R_1=R_2=R_3=40\Omega\)
\(U_{AB}=10V\)
______________________________
\(R_{tđ}=?;I=?;I_1=?I_2=?I_3=?\)
\(U_1=?;U_2=?;U_3=?\)
TH1 : \(R_1//\left(R_2ntR_3\right)\)
TH2 : \(R_2nt\left(R_3//R_1\right)\)
TH3 : R1 //R2//R3
GIẢI :
Trường hợp A :
R1 R2 R3 + - R1//(R2nối tiếp R3)
Điện trở tương đương toàn mạch là :
\(R_{tđ}=\dfrac{R_1.R_{23}}{R_1+R_{23}}=\dfrac{40.\left(40+40\right)}{40+80}\approx26,67\left(\Omega\right)\)
Cường độ đòng điện I là :
\(I=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{10}{26,67}\approx0,37\left(A\right)\)
Vì R1//R23 => \(U_{AB}=U_1=U_{23}=10V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{10}{40}=0,25\left(A\right)\)
\(I=I_1+ I_{23}\Rightarrow I_{23}=I-I_1=0,37-0,25=0,12\left(A\right)\)
Vì R2 ntR3 => \(I_2=I_3=I_{23}=0,12A\)
\(\left\{{}\begin{matrix}U_2=I_2.R_2=0,12.40=4,8\left(V\right)\\U_3=U_2=4,8\left(V\right)\end{matrix}\right.\)
Trường hợp B :
R2 R3 R1 A B
Vì R2 nt(R3//R1) nên :
\(R_{tđ}=R_2+\dfrac{R_3.R_1}{R_3+R_1}=40+\dfrac{40.40}{40+40}=60\left(\Omega\right)\)
Cường độ dòng điện I là :
\(I=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{10}{60}=\dfrac{1}{6}\left(A\right)\)
=> \(I=I_2=I_{31}=\dfrac{1}{6}\left(A\right)\)
\(U_2=I_2.R_2=\dfrac{1}{6}.40\approx6,67\left(V\right)\)
\(U_{31}=U_{AB}-U_2=3,33\left(V\right)\)
Mà : R3//R1 => \(U_{31}=U_3=U_1=3,33V\)
\(\left\{{}\begin{matrix}I_3=\dfrac{U_3}{R_3}=\dfrac{3,33}{40}=0,08325\left(A\right)\\I_1=I_3=0,08325\left(A\right)\end{matrix}\right.\)
Trường hợp C :
R1 R2 R3 + -
Vì R1//R2//R3 nên :
Điện trở tương đương toàn mạch là :
\(R_{tđ}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}}=\dfrac{1}{\dfrac{1}{40}+\dfrac{1}{40}+\dfrac{1}{40}}=\dfrac{40}{3}\left(\Omega\right)\)
\(U_{AB}=U_1=U_2=U_3=10V\)
Cường độ dòng điện I là :
\(I=\dfrac{U}{R_{tđ}}=\dfrac{10}{\dfrac{40}{3}}=0,75\left(A\right)\)
\(I_1=I_2=I_3=\dfrac{U_1}{R_1}=\dfrac{10}{40}=0,25\left(A\right)\)

a) Rtđ của đoạn mạch AB khi R1 mắc nối tiếp với R2 là: Rtđ = R1 + R2 = 20 + 20 = 40Ω.
Vậy Rtđ lớn hơn, mỗi điện trở thành phần.
b) Khi R1 mắc song song với R2 thì:
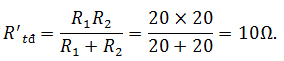
Vậy R'tđ nhỏ hơn mỗi điện trở thành phần.
c) Tỉ số giữa Rtđ và R'tđ là:
![]()

R1 R2 R Hình 1 A B R1 R2 R A B Hình 2 R A B Hình 3 Mk sẽ biến đổi hơi lằng nhằng tí nha!
gọi \(I_1\) là cường độ dòng điện khi mắc mạch như hình 1
gọi \(I_2\) là cường độ dòng điện khi mắc mạch như hình 2
\(P_1\) là công suất của R khi mắc mạch như hình 1
\(P_2\) là công suất của R khi mắc mạch như hình 2
Ta có
\(\dfrac{P_1}{P_2}=\dfrac{U.I_1}{U.I_2}\Rightarrow\dfrac{I_1}{I_2}=\dfrac{20}{80}=\dfrac{1}{4}\)
Mà cường độ dòng điện tỉ lệ nghịch với điện trở (với đk cùng 1 HĐT)
Nên \(\dfrac{I_1}{I_2}=\dfrac{R_{td2}}{R_{td1}}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{\dfrac{2}{3}R_2+R}{3R_2+R}=\dfrac{1}{4}\) (đây là mk tính R tương đương của 2 cách mắc rồi thay vào đó nha với đk của bài R1=2R2)
\(\Rightarrow4\left(\dfrac{2}{3}R_2+R\right)=3R_2+R\)
\(\Rightarrow R_2=9R\)
đến đây là ngon rồi!
ta tính được \(R_{td1}=3R_2+R=28R\)
và \(R_{td3}=R\)
\(\Rightarrow\dfrac{P_3}{P_1}=\dfrac{\dfrac{U^2}{R_{td3}}}{\dfrac{U^2}{R_{td1}}}=\dfrac{R_{td1}}{R_{td3}}\)
\(\Rightarrow\dfrac{P_3}{20}=\dfrac{28R}{R}=28\Rightarrow P_3=560W\)
Vậy công suất tiêu thụ trên R khi mắc như hình 3 là 560W.

a/ Rtd = R1 + R2 = 15 +30 = 45 Ω
I = \(\dfrac{U}{R_{td}}\) = \(\dfrac{9}{45}\) = 0,2 A = I1 = I2
U1 = I1 . R1 = 0,2 . 15 = 3 V
U2 = I2 . R2 = 0,2 . 30 = 6V
b/ Để đèn sáng bình thường thì:
U1 = Ud = 3 V
U2 = U - U1d = 9 - 3 = 6 V
Rd = \(\dfrac{U^2_d}{P_d}\) = \(\dfrac{3^2}{6}\) = 1,5 Ω
R1d = \(\dfrac{R_1.R_d}{R_1+R_d}\) = \(\dfrac{15.1,5}{15+1,5}\) = \(\dfrac{15}{11}\) Ω
I1d = \(\dfrac{U_{1d}}{R_{1d}}\) = \(\dfrac{3}{\dfrac{15}{11}}\) = 2,2 A = I2
R2 = \(\dfrac{U_2}{I_2}\) = \(\dfrac{6}{2,2}\) = \(\dfrac{30}{11}\) Ω \(\approx\) 2,73 Ω
+ Cm :
Nếu : R1 ntR2
\(P=P_1+P_2=U_1I+U_2I=I.R_1.I+I.R_2.I=I^2R_1+I^2R_2=I^2\left(R_1+R_2\right)=I^2.R_{tđ}\)(I=I1 =I2)
Nếu : R1//R2
\(P=P_1+P_2=U.I_1+U.I_2=U.\frac{U}{R_1}+U\frac{U}{R_2}=\frac{U^2}{R_1}+\frac{U^2}{R_1}=U^2.\left(\frac{1}{R_1}+\frac{1}{R_2}\right)=U^2.\frac{1}{R_{tđ}}=\frac{U^2}{R_{tđ}}\)
(U=U1=U2)