Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Nếu k là một hằng số thì (ku)’ = ku’
Thật vậy, ta có: (ku)' = k'u + ku' = 0.u + ku' = ku'
Do đạo hàm của hàm hằng bằng 0
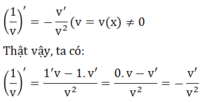

Gọi (un) và (an) là hai cấp số cộng có công sai lần lượt là \(d_1\) và d2 và có cùng n số hạng.
Ta có:
un = u1 + (n -1) d1
an = a1 + (n – 1)d2
⇒ un + an = u1 + a1 + (n – 1).(d1 + d2)
Vậy un + an là cấp số cộng có số hạng đầu là u1 + a1 và công sai là d1 + d2
Ví dụ:
1, 3, 5, 7 ,.... là cấp số cộng có công sai d1 = 2
0, 5, 10, 15,.... là cấp số cộng có công sai d2 = 5
⇒ 1, 8, 15, 22 ,... là cấp số cộng có công sai là d = d1 + d2 = 2 + 5 = 7

an= a1. q1n-1, q1 là hằng số
bn= \(b_1q_2^{n-1}\), q2 là hằng số
Khi đó: an.bn = = a1. q1n-1. b1. q1n-1 = (a1b1)(q1q2)n-1
Vậy dãy số anbn là một cấp số nhân có công bội : q = q1q2
Ví dụ:
1, 2, 4 ,... là cấp số nhân có công bội q1 = 2
3, 9, 27, .... là cấp số nhân có công bội q2 = 3
⇒ Suy ra: 3, 8, 108.. là cấp số nhân có công bội: q = q1q2 = 2.3 = 6

Giả sử có hai cấp số cộng (un) với công sai d1 và (vn) với công sai d2.
Xét dãy (an) với an = un + vn
Ta có: an + 1 – an = (un + 1 + vn + 1) – (un + vn)
= (un + d1 + vn + d2) – (un + vn)
= d1 + d2 = const
⇒(an) là cấp số cộng với công sai d1 + d2.
Ví dụ:
CSC (un): 1; 4; 7; 10; 13; 16; 19; …. có công sai d1 = 3 ;
CSC (vn): 4 ; 6 ; 8 ; 10 ; 12 ; 14 ; 16 … có công sai d2 = 2.
⇒ (an): 5; 10; 15; 20; 25; 30; 35; … có công sai d = 5.

Giả sử có hai cấp số nhân (un) với công bội q1 và (vn) với công bội q2.
Xét dãy số (an) với an = un.vn với mọi n ∈ N*.
Ta có:
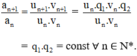
⇒ (an) là cấp số nhân với công bội q1.q2.
Ví dụ:
+ CSN (un) : 2 ; 4 ; 8 ; 16 ; 32 ; 64 ; … có công bội q1 = 2.
+ CSN (vn) : -1 ; 1 ; -1 ; 1 ; -1 ; 1 ; … có công bội q2 = -1.
⇒ CSN (an) : -2 ; 4 ; -8 ; 16 ; -32 ; 64 ; … có công bội q = -2.

Kí hiệu A là biến cố : "Quả lấy ra mầu đỏ"
B là biến cố : "Quả lấy ra ghi số chẵn"
a) Không gian mẫu \(\Omega=\left\{1,2,...,10\right\}\)
\(A=\left\{1,2,3,4,5,6\right\}\)
Từ đó : \(P\left(A\right)=\dfrac{6}{10}=\dfrac{3}{5}\)
Tiếp theo, \(B=\left\{2;4;6;8;10\right\}\) và \(A\cap B=\left\{2;4;6\right\}\)
Do đó : \(P\left(B\right)=\dfrac{5}{10}=\dfrac{1}{2};P\left(AB\right)=\dfrac{3}{10}\)
Ta thấy \(P\left(AB\right)=\dfrac{3}{10}=\dfrac{3}{5}.\dfrac{1}{2}=P\left(A\right)P\left(B\right)\)
Vậy A và B độc lập.

a) \(D = \left\{ {\left( {3;1} \right);\left( {3;2} \right);\left( {3;3} \right);\left( {3;4} \right);\left( {3;5} \right);\left( {3;6} \right)} \right\}\)
\(A{\rm{D}} = \left\{ {\left( {3;2} \right)} \right\};B{\rm{D}} = \left\{ {\left( {3;2} \right)} \right\};C{\rm{D}} = \left\{ {\left( {3;1} \right)} \right\}\)
b) \(\bar AB = \left\{ {\left( {1;6} \right);\left( {6;1} \right)} \right\}\)
\(\bar A{\rm{C}} = \left\{ {\left( {1;6} \right);\left( {6;1} \right);\left( {1;5} \right);\left( {5;1} \right);\left( {1;3} \right);\left( {3;1} \right);\left( {1;2} \right);\left( {2;1} \right);\left( {1;1} \right)} \right\}\)

Kí hiệu A là biến cố: "Quả lấy ra màu đỏ";
B là biến cố: "Quả lấy ra ghi số chẵn".
Không gian mẫu
Ω = {1, 2, ..., 10};
A = {1, 2, 3, 4, 5, 6}.
Từ đó: 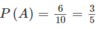
Tiếp theo: B = {2, 4, 6, 8, 10} và A ∩ B = {2, 4, 6}.
Do đó: 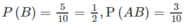
Ta thấy
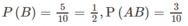
Vậy A và B độc lập.

Nếu E xảy ra tức là số chấm xuất hiện trên con xúc xắc bạn Minh gieo là số nguyên tố. Vì mỗi bạn một con xúc xắc nên \(P\left( B \right) = \frac{2}{6} = \frac{1}{3}\)
Nếu E không xảy ra tức là số chấm xuất hiện trên con xúc xắc bạn Minh gieo không là số nguyên tố. Vì mỗi bạn một con xúc xắc nên \(P\left( B \right) = \frac{2}{6} = \frac{1}{3}\)
Như vậy xác suất xảy ra của biến cố E không thay đổi bởi việc xảy ra hay không xảy ra của biến cố B.
Vì mỗi bạn một con xúc xắc nên \(P\left( E \right) = \frac{3}{6} = \frac{1}{2}\) dù biến cố B xảy ra hay không xảy ra
Vậy hai biến cố E và B độc lập.
Hai biến cố A và B được gọi là độc lập khi việc xảy ra hoặc không xảy ra của biến cố A không ảnh hưởng đến việc xảy ra hoặc không xảy ra của biến cố B và ngược lại
Vd: Biến cố A:"Chọn một số chẵn trong 5 số tự nhiên đầu tiên"
Biến cố B:"Chọn một số lẻ trong 5 số tự nhiên đầu tiên"