Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3)- theo bài tao có :A+B+C=180 độ.(định lí tổng ba góc của 1 tam giác)
C:B:A=1:3:6 => C/1=B/3=A/6=(A+B+C)/(1+3+6)=180/10=18
Do đó :C/1=18 B/3=18 A/6=18
=>C=18 độ =>B=54 độ =>A=104 độ

Bài 2:
\(\widehat{ADB}=180^0-80^0=100^0\)
Ta có: \(\widehat{ADB}+\widehat{BAD}+\widehat{B}=\widehat{ADC}+\widehat{CAD}+\widehat{C}\)
\(\Leftrightarrow\widehat{B}+100^0=\widehat{C}+80^0\)
\(\Leftrightarrow1.5\widehat{C}-\widehat{C}=-20^0\)
\(\Leftrightarrow\widehat{C}=40^0\)
hay \(\widehat{B}=60^0\)
=>\(\widehat{BAC}=80^0\)

a: Đặt số đo góc A là x
Số đo góc B là y
Số đo góc C là z
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: x=40; y=60; z=80

a/ Ta có: \(\widehat{A}\):\(\widehat{B}\):\(\widehat{C}\) = 1 : 2 : 3
=> \(\frac{\widehat{A}}{1}\)=\(\frac{\widehat{B}}{2}\)=\(\widehat{\frac{C}{3}}\) và góc A + góc B + góc C = 1800
Áp dụng tính chất dãy tỉ số bằng nhau
Ta có: \(\frac{\widehat{A}}{1}\)=\(\widehat{\frac{B}{2}}\)=\(\widehat{\frac{C}{3}}\)=\(\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+2+3}\)=\(\frac{180^0}{6}\)=300
\(\widehat{\frac{A}{1}}\)=300 => góc A = 300
\(\widehat{\frac{B}{2}}\)=300 => góc B = 600
\(\frac{\widehat{C}}{3}\)=300 => góc C = 900
Vậy 3 góc A, B, C lần lượt là 300; 600; 900
b/ Hình vẽ
A C B x
Bạn có viết sai đề không?? Phân giác góc ngoài tại đỉnh C làm sao cắt AB được
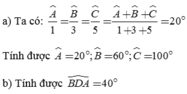
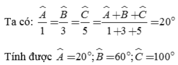

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: a=40; b=60; c=80