3 x 1 -...

Khách

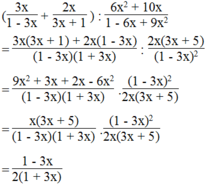
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

30 tháng 8 2018

3 x 1 - 3 x + 2 x 3 x + 1 : 6 x 2 + 10 x 1 - 6 x + 9 x 2

#Toán lớp 8

Cao Minh Tâm

30 tháng 8 2018

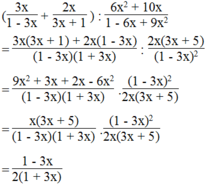
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Hồ Thu Phương

19 tháng 2 2016 - olm

1.giải các phương trình sau:

a, 3(2x+1)/4 - 5x+3/6 = 2x-1/3 - 3-x/4

b, 19/4 - 2(3x-5)/5 = 3-2x/10 - 3x-1/4

c, x-2*3/2+3 + x-3*5/3+5 + x-5*2/5+2 = 10

d, x-3/5*7 + x-5/3*7 + x-7/3*5 = 2(1/3 + 1/5 + 1/7)

2. giải các phương trình:

a, x-1/9 + x-2/8 = x-3/7 + x-4/6

b, (1/1*2 + 1/2*3 + 1/3*4 + ... + 1/9*10) (x-1) + 1/10x = x- 9/10

#Toán lớp 8

Nguyễn Huy Tú

9 tháng 1 2021

Câu 1 :

a, \(\frac{3\left(2x+1\right)}{4}-\frac{5x+3}{6}=\frac{2x-1}{3}-\frac{3-x}{4}\)

\(\Leftrightarrow\frac{6x+3}{4}+\frac{3-x}{4}=\frac{2x-1}{3}+\frac{5x+3}{6}\)

\(\Leftrightarrow\frac{5x+6}{4}=\frac{9x+1}{6}\Leftrightarrow\frac{30x+36}{24}=\frac{36x+4}{24}\)

Khử mẫu : \(30x+36=36x+4\Leftrightarrow-6x=-32\Leftrightarrow x=\frac{32}{6}=\frac{16}{3}\)

tương tự

Đúng(0)

Phan Nghĩa

16 tháng 5 2021

\(\frac{19}{4}-\frac{2\left(3x-5\right)}{5}=\frac{3-2x}{10}-\frac{3x-1}{4}\)

\(< =>\frac{19.5}{20}-\frac{8\left(3x-5\right)}{20}=\frac{2\left(3-2x\right)}{20}-\frac{5\left(3x-1\right)}{20}\)

\(< =>95-24x+40=6-4x-15x+5\)

\(< =>-24x+135=-19x+11\)

\(< =>5x=135-11=124\)

\(< =>x=\frac{124}{5}\)

Đúng(0)

Hạ Hân

22 tháng 8 2016 - olm

1.
(x-3)(x^2+3x+9)+x(x-2)(x+2)=1
2.
(x+1)^3-(x-1)^3-6(x-1)^2= -10

#Toán lớp 8

Ngọc Mai

15 tháng 2 2020

1) (3x-2)/3-2=(4x+1)/4
2) (x-3)/4+(2x-1)/3=(2-x)/6
3) 1/2 (x+1)+1/4 (x+3)=3-1/3 (x+2)
4) (x+4)/5-x+4=x/3-(x-2)/2
5) (4-5x)/6=2(-x+1)/2
6) (-(x-3))/2-2=5(x+2)/4
7)2(2x+1)/5-(6+x)/3=(5-4x)/15
8) (7-3x)/2-(5+x)/5=1
9)(x-1)/2+3(x+1)/8=(11-5x)/3
10)(3+5x)/5-3=(9x-3)/4

#Toán lớp 8

Trịnh Hồng Minh Châu

15 tháng 2 2020

Hỏi đáp Toán

Đúng(2)

DANG DINH DAM

15 tháng 2 2020

https://i.imgur.com/zKeoHqB.jpg

Đúng(0)

lê nhật duẫn

24 tháng 3 2020

bài 1: tìm x

a.(x-2)^2-(x-3)(x+3)=6

b. 4(x-3)^2-(2x-1)(2x+1)=10

c. (x-4)^2-(x-2)(x+2)=6

d. 9(x+1)^2-(3x-2)(3x+2)=10

#Toán lớp 8

Nguyễn Mạnh Nam

25 tháng 3 2020

Định làm mà mệt quá

Đúng(0)

quang ngo

16 tháng 8 2015 - olm

tìm x , biết :

a , (x-3)*(x^2+3x+9)+x(x+2)*(2-x)=1

b, (x+1)^3-(x-1)^3-6*(x-1)^2=-10

#Toán lớp 8

luuthianhhuyen

20 tháng 7 2017

câu a x = 7

Câu b x = -0,5

k nha

Đúng(0)

Nguyễn Việt Hoàng

20 tháng 7 2017

\(\text{a , (x-3).(x^2+3x+9)+x(x+2).(2-x)=1 }\)

=(x³-3³)+x(4-x²)=1

=x³-27+4x-x³=1

4x-27=1

4x=28

x=7

\(\text{b, (x+1)^3-(x-1)^3-6.(x-1)^2=-10}\)

=-0,5

Đúng(0)

bella nguyen

23 tháng 12 2016

Tìm x biết

a, ( x - 2)² - (x - 3)(x+3) = 6

b, 4( x - 3)² --(2x - 1)(2x + 1)= 10

c, ( x - 4)²- x (x -2(x + 2) = 6

d, 9( x + 1)^2 -(3x -2)(3x+ 2)= 10

#Toán lớp 8

Võ Đông Anh Tuấn

23 tháng 12 2016

a ) \(\left(x-2\right)^2-\left(x-3\right)\left(x+3\right)=6\)

\(\Leftrightarrow x^2-4x+4-x^2+9=6\)

\(\Leftrightarrow-4x+13=6\)

\(\Leftrightarrow-4x=-7\)

\(\Leftrightarrow x=\frac{7}{4}\)

Vậy \(x=1\).

b ) \(4\left(x-3\right)^2-\left(2x-1\right)\left(2x+1\right)=10\)

\(\Leftrightarrow4\left(x^2-6x+9\right)-\left(4x^2-1\right)=10\)

\(\Leftrightarrow4x^2-24x+36-4x^2+1=10\)

\(\Leftrightarrow-24x+37=10\)

\(\Leftrightarrow-24x=27\)

\(\Leftrightarrow x=\frac{9}{8}.\)

Mấy pài kia tương tự . :D

Đúng(0)

Phương Mai

23 tháng 12 2016

cậu khai triển các tích ra là ra thui mà cậu

Đúng(0)

Nguyễn Thị Kim Anh

23 tháng 7 2017 - olm

tìm x

a , (x+5)^2-(x-3)(x+3)=-15

b, (x-3)(x^2+3x+9)+x(x+2).(2-x)=1

c, (x+1)^3-(x-1)^3-6(x-1)^2=10

#Toán lớp 8

NTB OFFICIAL

1 tháng 7 2018

bài 1 : Rút gọn

8) x+3/x^2-3x

9) x-2/x-5÷(x-2)^2/x^2-25

10) 1÷(1-1/a)

11) (a+6/3a+9-1/a+3)÷a+2/27a

12) 6x+6/3x^2+3x

13) 3/x+3 -x-6/x^2+3x

14) (x/x+2+2/x-2+4x/x^2-4)×x^2-2x+4/x+2

#Toán lớp 8

Nguyễn Lê Phước Thịnh

15 tháng 7 2022

Bài 1:

8: \(=\dfrac{x+3}{x\left(x-3\right)}\)

9: \(=\dfrac{x-2}{x-5}\cdot\dfrac{\left(x-5\right)\left(x+5\right)}{\left(x-2\right)^2}=\dfrac{x+5}{x-2}\)

10: \(=1:\dfrac{a-1}{a}=\dfrac{a}{a-1}\)

12: \(=\dfrac{6\left(x+1\right)}{3x\left(x+1\right)}=\dfrac{2}{x}\)

13: \(\dfrac{3}{x+3}-\dfrac{x-6}{x\left(x+3\right)}\)

\(=\dfrac{3x-x+6}{x\left(x+3\right)}=\dfrac{2x+6}{x\left(x+3\right)}=\dfrac{2}{x}\)

Đúng(0)

Công Chúa Tình Yêu

7 tháng 6 2019 - olm

Tìm x:

a) (x - 3)(x^2 + 3x + 9) + x(x + 2)(2 - x) = 1

b) (x + 1)^3 - (x - 1)^3 - 6(x -1)^2 = -10

#Toán lớp 8

Kiệt Nguyễn

7 tháng 6 2019

a) \(\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=1\)

\(\Leftrightarrow x^3-3^3+x\left(4-x^2\right)=1\)

\(\Leftrightarrow x^3-27+4x-x^3=1\)

\(\Leftrightarrow-27+4x=1\)

\(\Leftrightarrow4x=1+27\)

\(\Leftrightarrow4x=28\)

\(\Leftrightarrow x=28:4\)

\(\Leftrightarrow x=7\)

Vậy phương trình có 1 nghiệm duy nhất là 7

Đúng(0)

Kiệt Nguyễn

7 tháng 6 2019

b) \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)

Biến đổi vế trái của phương trình

\(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=4\left(3x-1\right)\)

Phương trình thu được sau khi biến đổi

\(4\left(3x-1\right)=-2.5\)

\(\Leftrightarrow12x-4=-10\)

\(\Leftrightarrow12x=-6\)

\(\Leftrightarrow x=\frac{-1}{2}\)

Vậy nghiệm duy nhất của phương trình là \(\frac{-1}{2}\)

Đúng(0)

Lê Trang

11 tháng 12 2017 - olm

Tìm x biết

a, (x-2)^2 - (x-3)(x+3)=6

b, 4(x-3)^2 - (2x-1)(2x+1)=10

c,(x-4)^2 - (x+2)(x-2)=6

d, 9(x+1)^2 - (3x-2)(3x+2)=10

giúp mk nha 😉😉😉

#Toán lớp 8

VRCT_Ran Love Shinichi

11 tháng 12 2017

a, (x-2)^2 - (x-3)(x+3)=6

x^2-4x+4-(x^2-9)=6

x^2-4x+4-x^2+9=6

(x^2-x^2)-4x+13=6

-4x=-7

x=1,75

b, 4(x-3)^2 - (2x-1)(2x+1)=10

4(x^2-6x+9)-(4x^2-1)=10

4x^2-24x+36-4x^2+1=10

-24x+37=10

x=9/8

c,(x-4)^2 - (x+2)(x-2)=6

x^2-8x+16-(x^2-4)=6

x^2-8x+16-x^2+4=6

-8x+20=6

x=7/4

d, 9(x+1)^2 - (3x-2)(3x+2)=10

9(x^2+2x+1)-(9x^2-4)=10

9x^2+18x+9-9x^2+4=10

18x+13=10

x=-1/6

Đúng(0)

Doraemon

1 tháng 7 2018

\(a,\left(x-2\right)^2-\left(x-3\right)\left(x+3\right)=6\)

\(\left(x-2\right)^2-\left(x-3\right)\left(x+3\right)=6\)

\(-4x+13=6\)

\(-4x=6-13\)

\(-4x=-7\)

\(x=\frac{-7}{-4}\)

\(x=\frac{7}{4}\)

Vậy \(x=\frac{7}{4}\)

\(b,4\left(x-3\right)^2-\left(2x-1\right)\left(2x+1\right)=10\)

\(4\left(x^2-6x+9\right)-\left(4x^2-1\right)=10\)

\(4x^2-24x+36-4x^2+1=10\)

\(-24x+37=10\)

\(x=\frac{9}{8}\)

Vậy \(x=\frac{9}{8}\)

\(c,\left(x-4\right)^2-\left(x+2\right)\left(x-2\right)=6\)

\(x^2-8x+16-\left(x^2-4\right)=6\)

\(x^2-8x+16-x^2+4=6\)

\(-8x+20=6\)

\(x=\frac{7}{4}\)

Vậy \(x=\frac{7}{4}\)

\(d,9\left(x+1\right)^2-\left(3x-2\right)\left(3x+2\right)=10\)

\(9\left(x^2+2x+1\right)-\left(9x^2-4\right)=10\)

\(9x^2+18x+9-9x^2+4=10\)

\(18x+13=10\)

\(x=\frac{-1}{6}\)

Vậy \(x=\frac{-1}{6}\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP