Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
Giả sử theo kế hoạch mỗi ngày người đó dự định may $a$ khẩu trang.
ĐK: $a\in\mathbb{N}^*$
Thời gian dự định: $\frac{1000}{a}$ (ngày)
Thực tế:
Mỗi ngày người đó may: $a+30$ (khẩu trang)
Số ngày may: $\frac{1000}{a}-1$ (ngày)
Số khẩu trang thực tế:
$(a+30)(\frac{1000}{a}-1)=1000+170$
$\Leftrightarrow a^2+200a-30000=0$
$\Rightarrow a=100$
Vậy mỗi ngày người đó dự định may 100 khẩu trang.
Gọi số thợ và số ngày lần lượt là a,b
Theo đề, ta có hệ:
(a-3)(b+6)=ab và (a+2)(b-2)=ab
=>ab+6a-3b-18=ab và ab-2a+2b-4=ab
=>6a-3b=18 và -2a+2b=4
=>a=8 và b=10
Ket qua to1 lam duoc trong thang dau la420 sp
To2 lam duoc300sp
Gọi số thợ cần thiết là x (người),x ∈ N* , thời gian cần thiết là y (ngày), y > 0.
Coi toàn bộ công việc như một đơn vị công việc, thì một người thợ trong 1 ngày làm được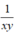 
( công việc).
Nếu giảm đi 3 người thì thời gian kéo dài 6 ngày. Như vậy, x – 3 người làm trong y + 6 ngày thì xong công việc. Do đó, ta có phương trình:
Nếu tăng thêm 2 người thì xong sớm 2 ngày. Như vậy, x + 2 người làm trong y – 2 ngày thì xong công việc. Do đó, ta có phương trình:
Từ (1) và (2) ta có hệ phương trình:
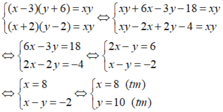
Vậy cần 8 người làm trong 10 ngày thì xong công việc.