Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật lý 8
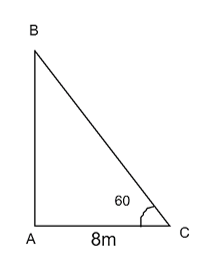
Gọi chân cây là A, đỉnh cây là B , điểm dài nhất bóng cây là C
Ta có góc BCA =60 độ
nên góc ABC =30 độ
Đối diện với cạnh góc vuông là 1 góc nhọn 30 độ thì cạnh góc vuông đó = 1/2 cạnh huyền
Do đó BC=2AC=2.4=8 (m)
Tam giác ABC vuông tại A áp dụng định lý Pytago ta có
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2=BC^2-AC^2=8^2-4^2\)
\(\Rightarrow AB^2=48\)
\(\Rightarrow AB=\sqrt{48}\)(m)
Vậy chiều cao cây dừa là căn 48m

Đáp án: ≈12 mét
Giải thích các bước giải:
Chiều cao của cây là 20.tan31≈12mét
\(\tan (C) = \dfrac{AB}{AC} \) ⇔ \(\tan (33) = \dfrac{AB}{40}\) ⇔ \(AB \) \(= 25,9 m\)

Chiều cao của cây:
\(h=20.tan30^0\approx12\left(m\right)\)

Chiều cao của cái cây đó là:
4,5*tan55\(\simeq6,43\left(m\right)\)

Gọi AC là chiều cao của cây, AB là bóng của cây trên mặt đất
Theo đề, ta có: AB vuông góc với AC tại A, AB=8,1m; \(\widehat{B}=55^0\)
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(AC=8.1\cdot tan55\simeq11,57\left(m\right)\)