Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình chính tắc của elip là: c) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\).
a) Không là PTCT vì a =b =8
b) Không là PTCT
d) Không là PTCT vì a =5 < b =8.

a) Đây là một parabol. Tiêu điểm của parabol có tọa độ là: \(F\left({\frac{9}{2};0} \right)\).
b) Đây là một elip. Tiêu điểm của elip có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right) = \left( { - \sqrt {39} ;0} \right)\\{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right) = \left( {\sqrt {39} ;0} \right)\end{array} \right.\)
c) Đây là một hyperbol. Tiêu điểm của hypebol có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right) = \left( { - 5;0} \right)\\{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right) = \left( {5;0} \right)\end{array} \right.\)

a) Phương trình \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 4,b = 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {3^2}} = 5\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
Tọa độ các đỉnh: \(A(0;3),B(4;0),C(0; - 3),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 6
b) Phương trình \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 8,b = 6 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{8^2} + {6^2}} = 10\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 10;0} \right),{F_2}\left( {10;0} \right)\)
Tọa độ các đỉnh: \(A(0;6),B(8;0),C(0; - 6),D( - 8;0)\)
Độ dài trục thực 16
Độ dài trục ảo 12
c) \({x^2} - 16{y^2} = 16 \Leftrightarrow \frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{1} = 1\)
Vậy ta có phương trình chính tắc của hypebol đã cho là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{1} = 1\)
Suy ra \(a = 4,b = 1 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {1^2}} = \sqrt {17} \)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - \sqrt {17} ;0} \right),{F_2}\left( {\sqrt {17} ;0} \right)\)
Tọa độ các đỉnh: \(A(0;1),B(4;0),C(0; - 1),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 2
d) \(9{x^2} - 16{y^2} = 144 \Leftrightarrow \frac{{{x^2}}}{{\frac{{144}}{9}}} - \frac{{{y^2}}}{{\frac{{144}}{{16}}}} = 1\)
Vậy ta có phương trình chính tắc của hypebol đã cho là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
Suy ra \(a = 4,b = 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {3^2}} = 5\)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
Tọa độ các đỉnh: \(A(0;3),B(4;0),C(0; - 3),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 6

ĐK: x khác 0
pt (2) \(\Leftrightarrow\left(x+\frac{1}{x}\right)^2+\left(y+\frac{1}{y}\right)^2=13\)
Đặt \(a=x+\frac{1}{x};b=y+\frac{1}{y}\), hệ pt trở thành:
\(\begin{cases}a+b=5\\a^2+b^2=13\end{cases}\) giải hệ pt đối xứng loại I được
\(\begin{cases}a=2\\b=3\end{cases}\) hoặc \(\begin{cases}a=3\\b=2\end{cases}\)
Thế vào được tập nghiệm của hệ pt đã cho:
\(\left\{\left(1;\frac{3-\sqrt{5}}{2}\right);\left(1;\frac{3+\sqrt{5}}{2}\right);\left(\frac{3-\sqrt{5}}{2};1\right);\left(\frac{3+\sqrt{5}}{2};1\right)\right\}\)
cam on minh da biet lam bai nay, truoc khi ban tra loi nen minh chua tick dung dau nhe ,mac du cach lam dung roi

Điều kiện \(x\ne0;y\ne0\)
Đặt \(x+\frac{1}{x}=a;y+\frac{1}{y}=b\), khi đó :
\(x^2+\frac{1}{x^2}=a^2-2;y^2+\frac{1}{y^2}=b^2-2\)
Thay vào hệ phương trình ta được :
\(\begin{cases}a+b=5\\a^2+b^2=13\end{cases}\)\(\Leftrightarrow\begin{cases}a+b=5\\\left(a+b\right)^2-2ab=13\end{cases}\)\(\Leftrightarrow\begin{cases}a+b=5\\ab=6\end{cases}\)
Do đó a và b là nghiệm của phương trình : \(t^2-5t+6=0\Leftrightarrow\begin{cases}t=2\\t=3\end{cases}\)
vậy \(\left(a;b\right)=\left(2;3\right);\left(a;b\right)=\left(3;2\right)\)
* Khi \(\begin{cases}a=2\\b=3\end{cases}\) ta có :
\(\begin{cases}x+\frac{1}{x}=2\\y+\frac{1}{y}=3\end{cases}\)\(\Leftrightarrow\begin{cases}x^2-2x+1=0\\y^2-3x+1=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=1\\y=\frac{3\pm\sqrt{5}}{2}\end{cases}\)
* Khi \(\begin{cases}a=3\\b=2\end{cases}\) ta có :
\(\begin{cases}x+\frac{1}{x}=3\\y+\frac{1}{y}=2\end{cases}\)\(\Leftrightarrow\begin{cases}x^2-3x+1=0\\y^2-2x+1=0\end{cases}\)\(\Leftrightarrow\begin{cases}y=1\\x=\frac{3\pm\sqrt{5}}{2}\end{cases}\)
Các nghiệm (x;y) là
\(\left(1;\frac{3+\sqrt{5}}{2}\right);\left(1;\frac{3-\sqrt{5}}{2}\right);\left(\frac{3+\sqrt{5}}{2};1\right);\left(\frac{3-\sqrt{5}}{2};1\right)\)

a) Ta có: \(a = 3,b = 4 \Rightarrow c = \sqrt {{3^2} + {4^2}} = 5\)
Vậy tiêu điểm của (E) là: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
b) Ta có: \(a = 6;b = 5 \Rightarrow c = \sqrt {{6^2} + {5^2}} = \sqrt {61} \)
Vậy tiêu điểm của (E) là: \({F_1}\left( { - \sqrt {61} ;0} \right),{F_2}\left( {\sqrt {61} ;0} \right)\)

Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
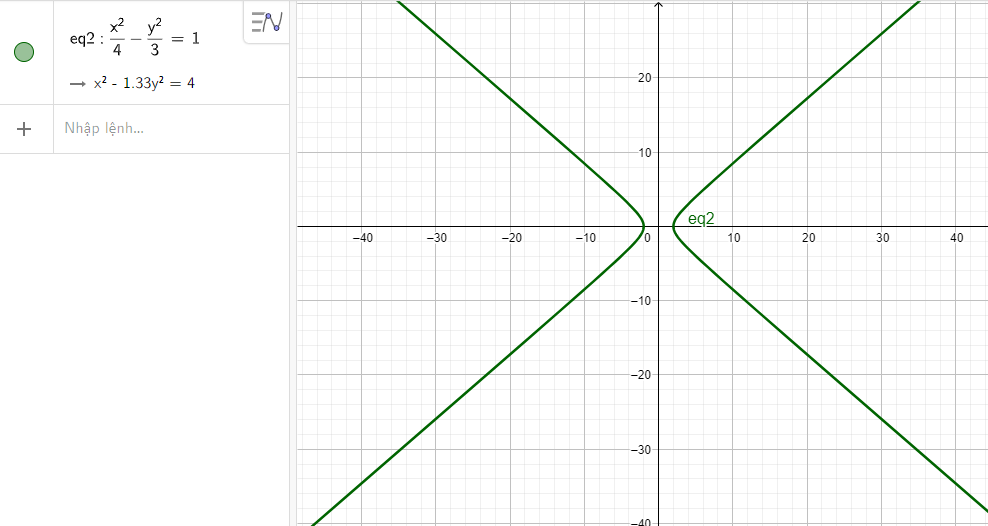
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

Những phương trình là phương trình chính tắc của (H) là: b), c), d).