K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CH
1
31 tháng 12 2023
\(\left(2x-3y\right)^{10}\)
\(=\left(2x\right)^{10}-C^1_{10}\cdot\left(2x\right)^9\cdot3y+C^2_{10}\cdot\left(2x\right)^8\cdot\left(3y\right)^2+...+\left(3y\right)^{10}\)
\(=1024x^{10}-1536x^9y+...+59049y^{10}\)
CM
10 tháng 6 2019
Chọn A
Số hạng tổng quát của biểu thức
x
-
2
x
2
21
,
x
≠
0
khi khai triển theo công thức nhị thức Newton là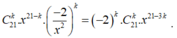 
Số hạng không chứa x trong khai triển nhị thức Newton
x
-
2
x
2
21
,
x
≠
0
là 
với k thỏa mãn
21-3k = 0 => k = 7
Vậy số hạng không chứa x trong khai triển nhị thức Newton
x
-
2
x
2
21
,
x
≠
0
là 
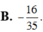
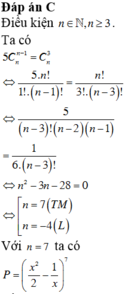
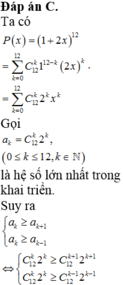
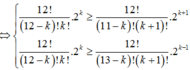
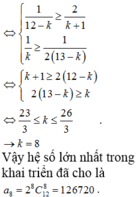
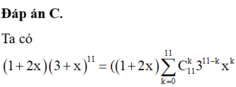
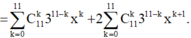
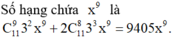
Tham khảo
Nhị thức Newton là 1 công thức khai triển hàm mũ của tổng. Cụ thể là khai triển một nhị thức bậc n thành một đa thức có n+1 số hạng.
Tham khảo:
Trong toán học, định lý khai triển nhị thức là một định lý toán học về việc khai triển hàm mũ của tổng. Cụ thể, kết quả của định lý này là việc khai triển một nhị thức bậc n thành một đa thức có {\displaystyle n+1} số hạng: {\displaystyle ^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}a^{k}}