Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m 2 ), điều kiện x ≥ 0, y ≥ 0, ta có x + y ≤ 0
Số công cần dùng là 20x + 30y ≤ 180 hay 20 + 3y ≤ 18
Số tiền thu được là
F = 3000000x + 4000000y (đồng)
Hay F = 3x + 4y (đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình
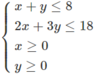
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
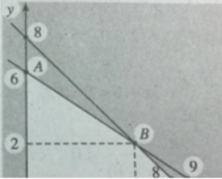
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.

So với tháng trước, đội đó vượt mức là :
(960:800)x 100%-100=20%
đs 20%
So với tháng trước, tháng này đội đó vượt mức là:
(960 : 800) x 100% - 100 = 20%
Đáp số: 20%.

a=120 nhé
gọi số cây giống cần tìm là a
\(\Rightarrow a\in BC\left(10;12;20\right)\)
\(10=2.5\)
\(12=2^2.3\)
\(20=2^2.5\)
\(BCNN\left(10;12;20\right)=2^2.3.5=60\)
BC(10;12;20) = B(60) = { 0;60;120;180;240;... }
Vì : \(100\le a\le150\) nên a = 180
Vậy số cây giờ cần mua là 180 cây