Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B
Gọi số proton, nơtron và electron của X là p, n và e (trong đó p = e)
Theo bài ra ta có hệ phương trình:
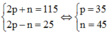
=> Cấu hình nguyên tử của X là
![]()

\(\left\{{}\begin{matrix}P+N+E=115\\P=E\\N-P=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2P+N=115\\N-P=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}P=E=35\\N=45\end{matrix}\right.\\ \Rightarrow A=P+N=35+45=80\left(đ.v.C\right)\)

Cho biết số liệu nguyên tử của nguyên tố x là 13 electron và số proton lớn hơn electron và lớp electron nằm trong nguyên tử

Bài 1:
\(a,\\ \left\{{}\begin{matrix}P+N+E=115\\\left(P+E\right)-N=25\\P=E\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2P+N=115\\2P-N=25\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}P=E=Z=35\\N=45\end{matrix}\right.\\ b,\dfrac{N}{P}=\dfrac{45}{35}=\dfrac{9}{7}\approx1,29\\ \Rightarrow N>P\)
1.
a. Ta có: n + p + e = 115
Mà p = e, nên: 2p + n = 115 (1)
Theo đề, ta có: 2p - n = 25 (2)
Từ (1) và (2), ta có HPT:
\(\left\{{}\begin{matrix}2p+n=115\\2p-n=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=90\\2p-n=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=45\\p=35\end{matrix}\right.\)
Vậy p = e = 35 hạt, n = 45 hạt.
=> Số khối của R = p + e = 45 + 35 = 80 đvC
b. Tỉ lệ của n và p là: \(\dfrac{n}{p}=\dfrac{45}{35}=\dfrac{9}{7}\)

Ta có: \(\left\{{}\begin{matrix}p+e+n=58\\p=e\\p+e-n=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=40\\2p+n=58\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=19\\n=20\end{matrix}\right.\)

Tổng số hạt proton, nơtron, electron trong một loại nguyên tử của nguyên tố Y là 54
⇒ p + e + n = 54
do (p = e) \(\Rightarrow\) 2p + n = 54 (1)
Vì tổng số hạt mang điện gấp 1,7 lần số hạt ko mang điện
⇒ p + e = 1,7n
⇔ 2p - 1,7n = 0 (2)
Từ (1) và (2) \(\Rightarrow\)p = e = 17 ; n = 20

Đáp án D
Giả sử số hiệu nguyên tử, số nơtron của R lần lượt là Z, N.
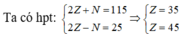
→ Cấu hình electron của R là 35R: [Ar] 3d104s24p5
Ta có: \(\left\{{}\begin{matrix}p+e+n=115\\p=e\\p+e-n=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=35\\n=45\end{matrix}\right.\)