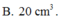Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
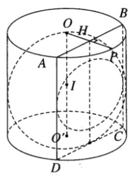
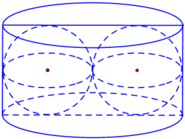
Vì các mặt đáy của hình trụ vuông góc với trục OO’ tại O và O’ nên chúng tiếp xúc với mặt cầu đường kính OO’.
Gọi I là trung điểm của đoạn OO’. Ta có I là tâm của mặt cầu. Kẻ IM vuông góc với một đường sinh nào đó (M nằm trên đường sinh) ta đều có IM = r là bán kính của mặt trụ đồng thời điểm M cũng thuộc mặt cầu. Vậy mặt cầu tiếp xúc với tất cả các đường sinh của mặt trụ.
Đáp án C
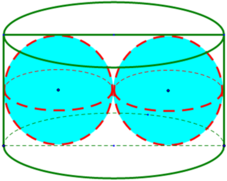
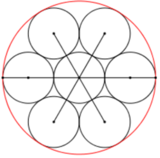
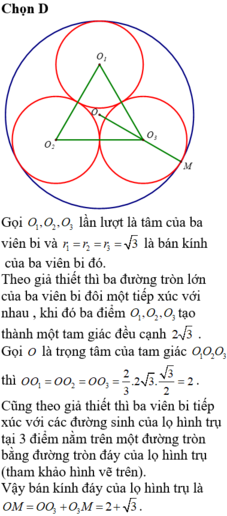
Do chiều cao của hình trụ là 2r nên để đựng được ba quả cầu trong hình trụ thì ba quả đó phải chạm đáy hình trụ. Khi đó gọi A,B,C là ba tâm của ba quả cầu thì tam giác ABC đều và bán kính R không nhỏ hơn bán kính đường tròn ngoại tiếp tam giác ABC cộng với bán kính r. Tam giác ABC có cạnh 2r nên ta có:
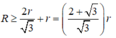
Đáp án B
Cách giải:
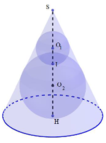
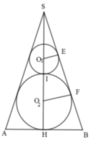
Ta có: O1E ⊥ SB, O2E ⊥ SB ⇒ O1E//O2E
Mà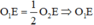 
là đường trung bình của tam giác SO2F
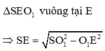
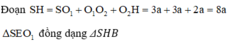
⇒ SO1 = O1O2 = a + 2a = 3a