Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
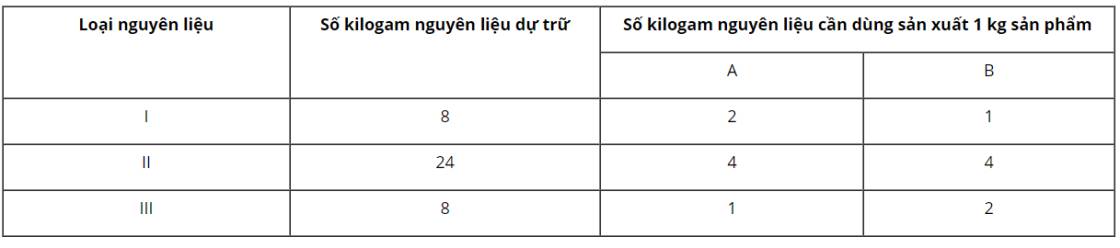
Gọi x, y lần lượt là số kilogam sản phẩm loại A, loại B mà công ty đó sản xuất.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Nguyên liệu loại I có số kilogam dự trữ là 8 kg nên \(2x + y \le 8\)
- Nguyên liệu loại II có số kilogam dự trữ là 24 kg nên \(4x + 4y \le 24\)
- Nguyên liệu loại III có số kilogam dự trữ là 8 kg nên \(x + 2y \le 8\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}2x + y \le 8\\4x + 4y \le 24\\x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.
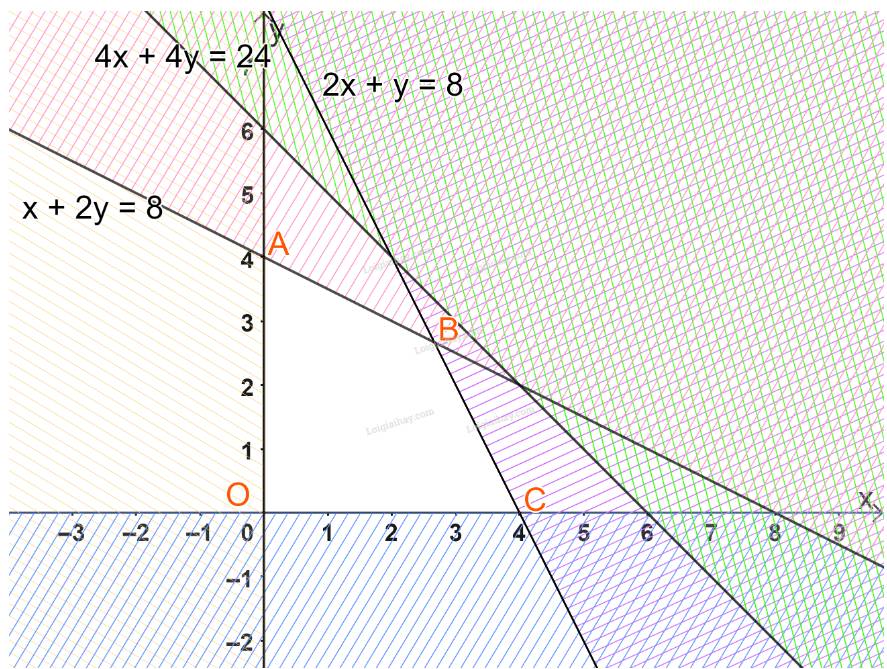
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(0;4),\)\(B(\frac{8}{3};\frac{8}{3}),\)\(C(4;0).\)
Gọi F là số tiền lãi (đơn vị: triệu đồng) thu về, ta có: \(F = 30x + 50y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 30.0 + 50.0 = 0\)
Tại \(A(0;4),\)\(F = 30.0 + 50.4 = 200\)
Tại \(B(\frac{8}{3};\frac{8}{3}),\)\(F = 30.\frac{8}{3} + 50.\frac{8}{3} = \frac{{640}}{3}\)
Tại \(C(4;0):\)\(F = 30.4 + 50.0 = 120\)
F đạt giá trị lớn nhất bằng \(\frac{{640}}{3}\) tại \(B(\frac{8}{3};\frac{8}{3}).\)
Vậy công ty đó nên sản xuất \(\frac{8}{3}kg\) sản phẩm mỗi loại để tiền lãi thu về lớn nhất.

Chọn C
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 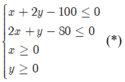
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0
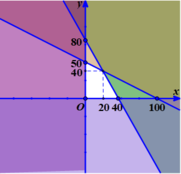
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 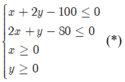
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0

Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.

+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 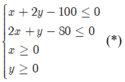
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0

Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.