
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
RO
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
3 tháng 9 2017
Đáp án B.
Đặt 3x = t > 0.
Phương trình <=> t2 + 2(x – 2)t + 2x – 5 = 0
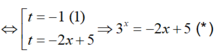
Có f(x) = 3x là hàm số đồng biến trên ℝ
g(x) = –2x + 5 là hàm số nghịch biến trên ℝ
=> Phương trình (*) ó f(x) = g(x) có nhiều nhất l nghiệm
Có f(1) = g(1) => x = 1 là nghiệm của phương trình.

CM
27 tháng 8 2018
Đáp án B
Đặt t = 2x > 1
PT
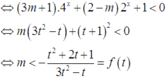
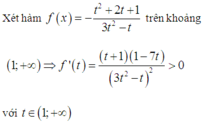
Dựa vào bảng biến thiên, suy ra m < -2
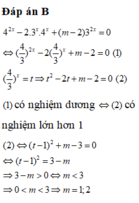




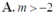
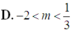
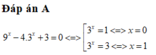



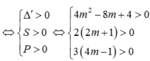

Lời giải:
Ta có:
\(2.16^x-(3+\sqrt{2})12^x+(1+\sqrt{2}).9^x=0\)
\(\Leftrightarrow 2\left(\frac{16}{9}\right)^x-(3+\sqrt{2})\left(\frac{12}{9}\right)^x+1+\sqrt{2}=0\)
\(\Leftrightarrow 2\left(\frac{4}{3}\right)^{2x}-(3+\sqrt{2})\left(\frac{4}{3}\right)^x+1+\sqrt{2}=0\)
Đặt \(\left(\frac{4}{3}\right)^x=t\Rightarrow 2t^2-(3+\sqrt{2})t+1+\sqrt{2}=0\)
\(\Rightarrow t=1\) hoặc \(t=\frac{1+\sqrt{2}}{2}\) (đều thỏa mãn)
Nếu \(t=1\Leftrightarrow \left(\frac{4}{3}\right)^x=1\Leftrightarrow x=0\)
Nếu \(t=\frac{1+\sqrt{2}}{2}\Leftrightarrow \left(\frac{4}{3}\right)^x=\frac{1+\sqrt{2}}{2}\)
\(\Leftrightarrow x= \log_{\frac{4}{3}}\frac{1+\sqrt{2}}{2}\)