K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
Vì \(\forall a \in \mathbb{Z}:a = \dfrac{a}{1}\)
Hoặc: \(a \in \mathbb{Z} \subset \mathbb{Q}\) => mỗi số nguyên cũng là một phân số.
b) Mệnh đề "Tập hợp các số thực chứa tập hợp các số hữu tỉ" là mệnh đề đúng.
c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.
Ví dụ: \(\sqrt 2 \) ( vì \(\sqrt 2 \in \mathbb{R};\;\sqrt 2 \notin \mathbb{Q}\)).

16 tháng 5 2017
a) \(\exists a\in\mathbb{Z}:a=a^2\)
b) \(\forall x\in\mathbb{R}:x+0=x\)
c) \(\exists x\in\mathbb{Q}:x< \dfrac{1}{x}\)
d) \(\forall n\in\mathbb{N}:n>0\)

HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) \(\exists x \in \mathbb{Z},\;x \not{\vdots} \;x.\)
b) \(\forall x \in \mathbb{R},\;x + 0 = x.\)
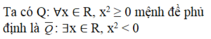
Ví dụ về tập hợp: Toàn bộ học sinh lớp 10A
a) 3 ∈ Z
b) √2 ∉ Q