Nếu tam giác ABC vuông tại C và có sinA = 2/3 thì tgB bằng: ( A ) 3 5 (...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

5 tháng 12 2018

Nếu tam giác ABC vuông tại C và có sinA = 2/3 thì tgB bằng:

( A ) 3 5 ( B ) 5 3 ( C ) 2 5 ( D ) 5 2

#Toán lớp 9

Cao Minh Tâm

5 tháng 12 2018

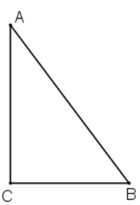
Giải bài 4 trang 134 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

12 tháng 2 2018

Nếu tam giác ABC vuông tại C và có sinA = 2/3 thì tgB bằng:

( A ) 3 5 ( B ) 5 3 ( C ) 2 5 ( D ) 5 2

#Toán lớp 9

Cao Minh Tâm

12 tháng 2 2018

Giải bài 4 trang 134 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng(0)

Sách Giáo Khoa

25 tháng 4 2017

Nếu tam giác ABC vuông tại C và có $\sin A=\dfrac{2}{3}$ thì tgB bằng : (A) $\dfrac{3}{5}$ (B) $\dfrac{\sqrt{5}}{3}$ (C) $\dfrac{2}{\sqrt{5}}$ (D) $\dfrac{\sqrt{5}}{2}$ Hãy chọn câu trả lời đúng...

Đọc tiếp

#Toán lớp 9

VinZoi Couple

25 tháng 4 2017

Trong tam giác vuông ABC $($\widehat{C}=90^o$)$ , ta có:

$sinA=BC/AB=2/3\RightarrowAB=3/2 BC$

Áp dụng định lí Py-ta-go trong tam giác vuông ABC, ta có:

$AC=\sqrt{AB^2-BC^2}=\sqrt{\left(\dfrac{3}{2}BC\right)^2-BC^2}=\dfrac{BC\sqrt{5}}{2}$

Ta có:

$\tan B=\dfrac{AC}{BC}=\dfrac{\dfrac{BC\sqrt{5}}{2}}{BC}=\dfrac{\sqrt{5}}{2}$

Chọn đáp án D

Đúng(0)

Khùng Điên

25 tháng 4 2017

Giải bài 4 trang 134 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng(0)

Anh Quynh

9 tháng 10 2021

Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA

#Toán lớp 9

Nguyễn Hoàng Minh

9 tháng 10 2021

$\sin^2\widehat{A}+\cos^2\widehat{A}=1\Leftrightarrow\cos^2\widehat{A}=1-\left(\dfrac{3}{5}\right)^2=1-\dfrac{9}{25}=\dfrac{16}{25}\\ \Leftrightarrow\cos\widehat{A}=\dfrac{4}{5}\\ \tan\widehat{A}=\dfrac{\sin\widehat{A}}{\cos\widehat{A}}=\dfrac{3}{4}\\ \Rightarrow\cot\widehat{A}=\dfrac{1}{\tan\widehat{A}}=\dfrac{4}{3}$

Đúng(3)

Anh Quynh

8 tháng 10 2021

Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA.

#Toán lớp 9

Anh Quynh

9 tháng 10 2021

Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA.

#Toán lớp 9

dương vũ

12 tháng 7 2017 - olm

Cho tam giác ABC vuông tại A , AB = 3√3 (cm) , AC=2√5 (cm). Tính BC và các góc B,C

#Toán lớp 9

Nhã Hy

12 tháng 7 2017

$\Delta ABC\left(\widehat{A}=90^0\right)$

$BC^2=AB^2+AC^2$

$BC^2=\left(3\sqrt{3}\right)^2+\left(2\sqrt{5}\right)^2=47$

$\Rightarrow BC=\sqrt{47}\left(cm\right)$

$\sin\widehat{C}=\frac{3\sqrt{3}}{\sqrt{47}}\Rightarrow\widehat{C}\approx55^0$

$\widehat{B}=90^0-\widehat{C}$(2 góc phụ nhau)

$\widehat{B}=90^0-55^0=35^0$

Chúc bạn học tốt.

Đúng(0)

dương vũ

12 tháng 7 2017

cảm ơn bạn

Đúng(0)

Kiến Thành

24 tháng 6 2021

Cho tam giác ABC vuông tại A có AB bằng 3 cm BC = 5 cm a tính AC, góc B góc c b) phân giác của góc A cắt BC tại E Tính BE CE d)kẻ đường c kẻ đường cao AH và đường trung tuyến AM tính diện tích tam giác AMH

#Toán lớp 9

Nguyễn Lê Phước Thịnh

24 tháng 6 2021

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

$AB^2+AC^2=BC^2$

$\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16$

hay AC=4(cm)

Vậy: AC=4cm

Đúng(2)

Nguyễn Lê Phước Thịnh

24 tháng 6 2021

b) Xét ΔABC có AE là tia phân giác ứng với cạnh BC(gt)

nên $\dfrac{BE}{AB}=\dfrac{CE}{AC}$(Tính chất tia phân giác của tam giác)

hay $\dfrac{BE}{3}=\dfrac{CE}{4}$

mà BE+CE=BC=5cm(gt)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

$\dfrac{BE}{3}=\dfrac{CE}{4}=\dfrac{BE+CE}{3+4}=\dfrac{BC}{7}=\dfrac{5}{7}$

Do đó:

$\left\{{}\begin{matrix}\dfrac{BE}{3}=\dfrac{5}{7}\\\dfrac{CE}{4}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BE=\dfrac{15}{7}\left(cm\right)\\CE=\dfrac{20}{7}\left(cm\right)\end{matrix}\right.$
Vậy: $BE=\dfrac{15}{7}cm;CE=\dfrac{20}{7}cm$

Đúng(1)

Kamado Tanjirou ๖ۣۜ( ๖ۣۜTεαм ƙɦĭêηɠ...

30 tháng 10 2021

Cho tam giác ABC vuông tại A, đường cao AH.

a) Nếu sin ACB=3/5 và BC=20 cm. Giải tam giác ABC.

b) Đường thẳng vuông góc với BC tại B cắt đường thẳng AC tại D. c/m AD.AC=BH.BC

c) Kẻ tia phân giác BE của DBA . c/m $tanEBA=\dfrac{AD}{AB+BD}$

#Toán lớp 9

Nguyễn Lê Phước Thịnh

30 tháng 10 2021

b: Xét ΔABC vuông tại A có AH là đường cao

nên $BH\cdot BC=AB^2\left(1\right)$

Xét ΔBCD vuông tại B có BA là đường cao

nên $AD\cdot AC=AB^2\left(2\right)$

Từ (1) và (2) suy ra $BH\cdot BC=AD\cdot AC$

Đúng(0)

Thầy giáo dạy Toán

11 tháng 11 2015 - olm

Cho tam giác ABC vuông tại A; BC = 10 đường cao AH

1, Nếu sin góc ACB = 3/5. Tính AB; AC; BH và giá trị biểu thức P = 3. sin góc BAH + 2 tan HAC
2, Lấy M tùy ý trên cạnh BC. Gọi E, F lần lượt là hình chiếu M trên AB, AC. CMR: AE.EB + AF.FC = BM.MC

3, Đặt ABC = a. Tính giá trị lớn nhất của S = 3 sina + 4 cosa

#Toán lớp 9

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP